.webp)
Matriks adalah susunan bilang-bilangan dalam bentuk persegi panjang yang disusun berdasarkan baris dan kolom. Bilangan yang disusun dalam baris dan kolom tersebut dinamakan elemen-elemen penyusun matriks.
Matriks merupakan salah satu materi pelajaran Matematika yang akan kamu temui di kelas XI atau 2 SMA. Dalam matriks dikenal juga transpose matriks seperti yang akan kita bahas dalam artikel ini, nih.
Pengertian Transpose Matriks
Transpose matriks adalah matriks baru yang diperoleh dengan cara menukar elemen-elemen baris menjadi elemen kolom atau sebaliknya.
SCROLL TO CONTINUE WITH CONTENT
Sementara pengertian matriks itu sendiri adalah susunan bilangan yang terdiri atas baris dan kolom dan ditulis dalam kurung ().
Sebagai contoh,
 Contoh matriks transpose Foto: Ist |
Dikutip dari e-Modul Kemdikbud Matematika Kelas XI: Matriks yang disusun oleh Dyah Astuti, transpose matriks memiliki sifat-sifat sebagai berikut.
1. (A + B)T = (A)T + (B)T
2. (AT)T = A
3. (AB)T = (A)T (B)T
4. (kA)T = k.AT, dengan k = konstanta
Cara Mengerjakan Transpose Matriks
Sebelum mengerjakan contoh soal transpose matriks, kamu perlu mengenal ordo matriks, yakni ukuran matriks yang dinyatakan dalam suatu baris x kolom. Jika diketahui suatu matriks A memiliki m baris dan n kolom, matriks A berukuran atau berordo m x n yang bisa ditulis dengan Amxn.
Nah, untuk memahami lebih lanjut mengenai transpose matriks, perhatikan contoh-contoh soal di bawah ini beserta cara pengerjaannya, yuk!
1. Tuliskan transpose matriks A jika diketahui, matriks A 3x2
 Contoh matriks transpose Foto: Ist |
Pembahasannya sebagai berikut,
Matriks A memiliki elemen dengan susunan:
baris pertama: a dan b
baris kedua: c dan d
baris ketiga: e dan f
kolom pertama: a, c, dan e
kolom kedua: b, d, dan f
Maka, susunan transpose matriks A adalah:
baris pertama: a, c, dan e
baris kedua: b, d, dan f
kolom pertama: a dan b
kolom kedua: c dan d
kolom ketiga: e dan f
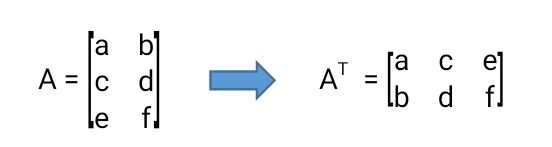 Contoh penyelesaian soal matriks transpose Foto: Ist |
Baca juga: Mengapa Satu Jam 60 Menit? |
(pal/pal)
