Dalam pelajaran matematika, kita mempelajari bab Matriks. Matriks persegi 2x2 cenderung mudah dipahami, namun matriks 3x3 mungkin agak membingungkan bagi sebagian orang.
Untuk mencari determinan matriks 3x3, kita bisa menggunakan metode Sarrus maupun Kofaktor. Di bawah ini akan kita ulas cara mengerjakan dengan dua metode tersebut, beserta contoh soalnya.
Mencari Determinan Matriks 3x3
Dilansir dari buku Modul Pembelajaran SMA Matematika Umum Kelas XI: Determinan dan Invers Matriks dari situs Kemdikbud, berikut ini cara mencari determinan matriks 3x3 dengan metode Sarrus dan Kofaktor:
SCROLL TO CONTINUE WITH CONTENT
Metode Sarrus
Untuk mencari determinan matriks 3x3 dengan metode Sarrus, kita harus mengetahui terlebih dahulu strukturnya terlebih dahulu. Misalnya matriks A ditulis sebagai berikut:
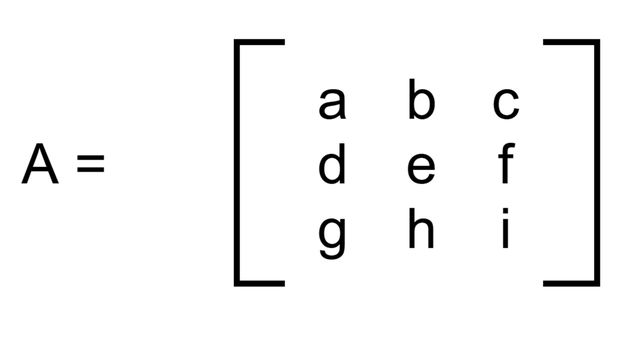 Contoh matriks A. Foto: detikcom/Bayu Ardi Isnanto Contoh matriks A. Foto: detikcom/Bayu Ardi Isnanto |
Kemudian determinan A atau Det A atau yang disimbolkan |A| dapat dicari dengan menambahkan kolom pertama dan kedua ke sebelah kanan matriks menjadi seperti ini:
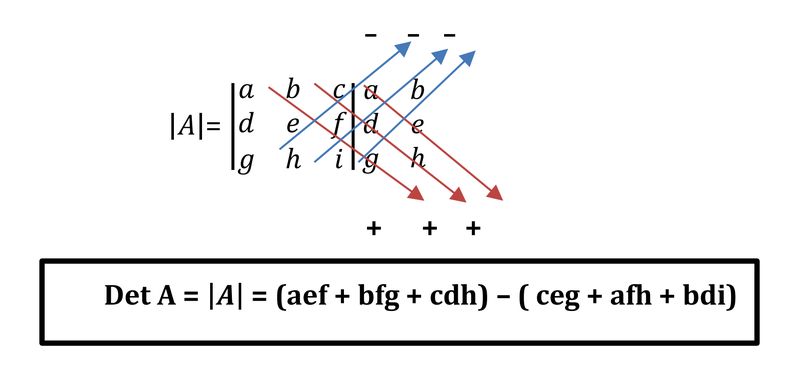 Rumus determinan matriks metode Sarrus. Foto: dok Modul Pembelajaran SMA Matematika Umum Kelas XI: Determinan dan Invers Matriks Rumus determinan matriks metode Sarrus. Foto: dok Modul Pembelajaran SMA Matematika Umum Kelas XI: Determinan dan Invers Matriks |
Contoh Soal:
Diketahui matriks A memiliki nilai sebagai berikut:
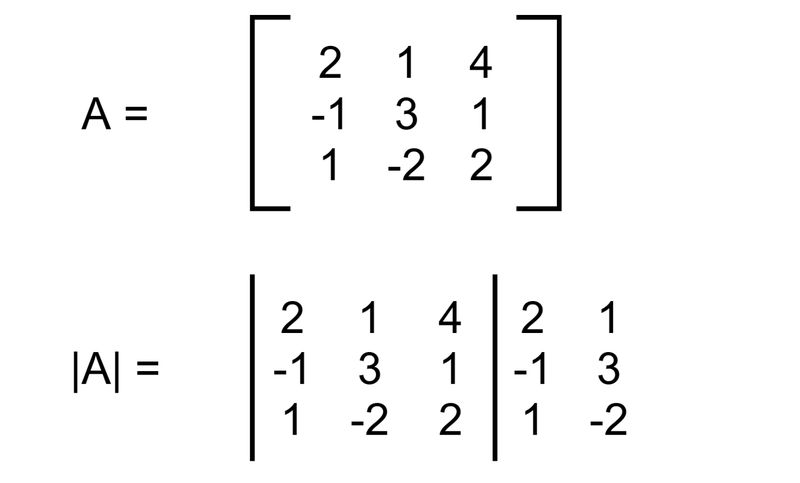 Contoh soal matriks. Foto: detikcom/Bayu Ardi Isnanto Contoh soal matriks. Foto: detikcom/Bayu Ardi Isnanto |
|A| = (aef + bfg + cdh) - (ceg + afh + bdi)
|A| = {(2)(3)(2) + (1)(1)(1) + (4)(-1)(-2)} - {(4)(3)(1) + (2)(1)(-2) + (1)(-1)(2)}
|A| = (12+1+8) - (12-4-2)
|A| = 21 - 6
|A| = 15
Maka determinan matriks A adalah 15.
Metode Kofaktor
Struktur matriks pada metode Kofaktor sebetulnya sama dengan metode di atas, namun akan lebih mudah dipahami jika dibuat seperti ini:
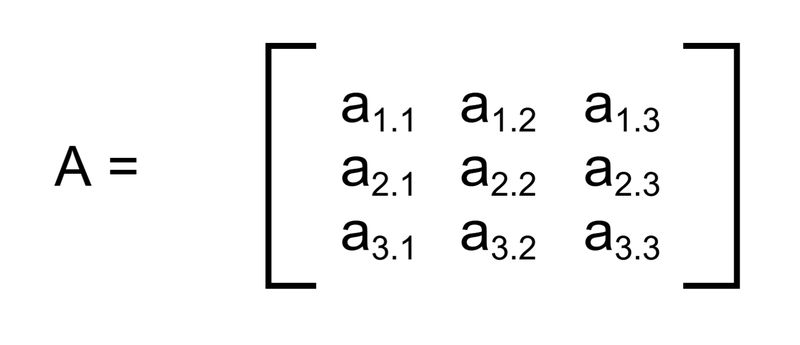 Struktur matriks metode Kofaktor. Foto: detikcom/Bayu Ardi Isnanto Struktur matriks metode Kofaktor. Foto: detikcom/Bayu Ardi Isnanto |
Metode Kofaktor dirumuskan sebagai −1 pangkat baris ditambah kolom elemen minor dari matriks bersangkutan. Secara matematis dirumuskan sebagai :
𝐾𝑖𝑗 = (-1)𝑖+𝑗. 𝑀𝑖𝑗
Sedangkan rumus determinannya yaitu:
|A| = ∑ ai.j x Ki.j
Keterangan :
i = baris
j = kolom.
𝐾𝑖𝑗 = kofaktor dari suatu matriks baris ke-i dan kolom ke-j.
𝑀𝑖𝑗 = minor baris ke-i kolom ke-j dari suatu matriks.
a𝑖𝑗 = nilai pada baris ke-i kolom ke-j dari suatu matriks.
Contoh Soal:
Kita misalkan matriks A dengan nilai yang sama dengan contoh sebelumnya.
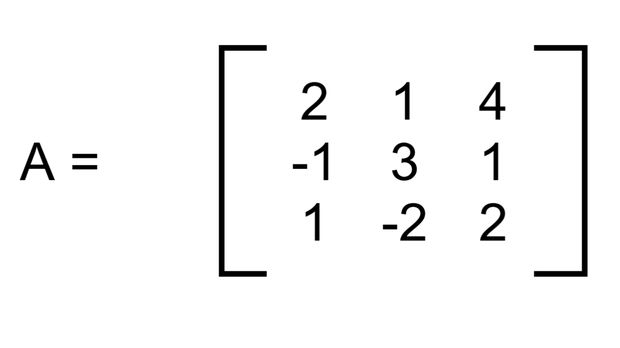 Contoh soal matriks. Foto: detikcom/Bayu Ardi Isnanto Contoh soal matriks. Foto: detikcom/Bayu Ardi Isnanto |
Kemudian kita pilih salah satu elemen baris. Misalnya kita pilih baris ke-1, yaitu:
a1.1 = 2
a1.2 = 1
a1.3 = 4
 Contoh soal matriks metode Kofaktor. Foto: dok E-Modul Matematika Kelas XI: Determinan dan Invers Matriks Contoh soal matriks metode Kofaktor. Foto: dok E-Modul Matematika Kelas XI: Determinan dan Invers Matriks |
Maka nilai determinan A menggunakan metode Kofaktor juga sama dengan metode Sarrus, yaitu 15.
Demikian tadi cara mengerjakan soal determinan matriks 3x3 dengan mudah menggunakan metode Sarrus dan Kofaktor.
Baca juga: 12 Jenis Matriks Lengkap dengan Contohnya |
(bai/row)


























































