Materi persamaan garis lurus umumnya kita dapatkan dalam pelajaran matematika di bangku SMP. Garis lurus merupakan garis dengan kemiringan yang stagnan atau sama pada setiap ruasnya.
Jika dilihat pada grafik, persamaan garis lurus memiliki perbandingan yang sama. Artinya antara selisih koordinat y dan selisih koordinat x bernilai serupa. Maka, persamaan garis lurus adalah perbandingan selisih koordinat y dan selisih koordinat x.
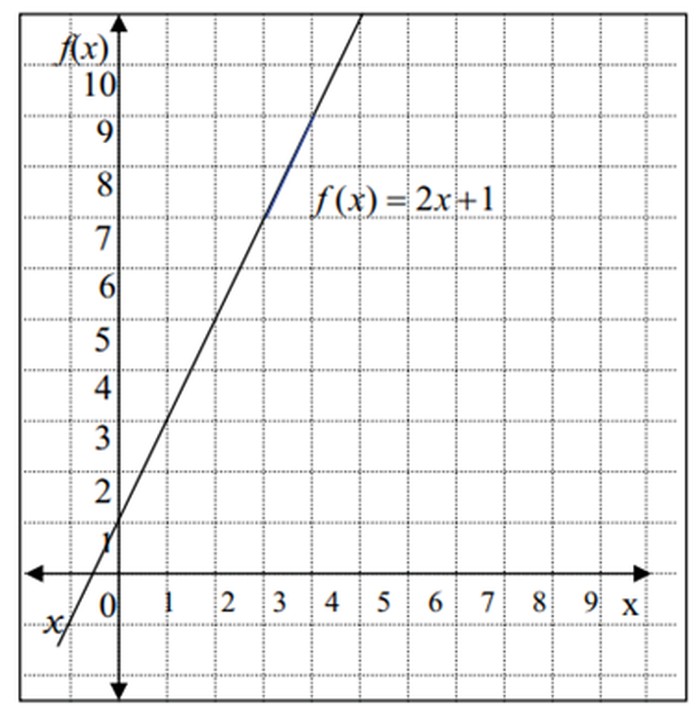
Dikutip dari Modul Persamaan Garis Lurus yang disusun oleh Atmini Dhoruri, konsep persamaan garis lurus berkaitan dengan gradien atau kemiringan. Biasanya persamaan garis lurus digambarkan dalam bidang kartesius. Untuk memahami pengertian persamaan garis lurus, perhatikan grafik dalam koordinat cartesius berikut ini.
SCROLL TO CONTINUE WITH CONTENT
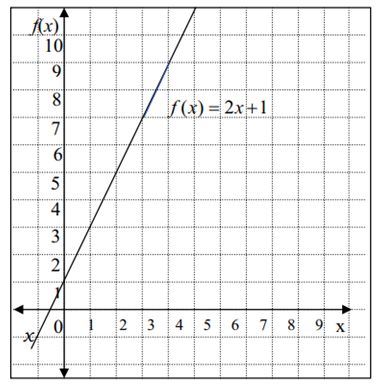 Grafik koordinat cartesius. Foto: Modul Persamaan Garis Lurus yang disusun oleh Atmini Dhoruri Grafik koordinat cartesius. Foto: Modul Persamaan Garis Lurus yang disusun oleh Atmini Dhoruri |
Pada grafik di atas diketahui fungsi f(x) = 2x + 1. Sumbu mendatar disebut sumbu x dan sumbu tegak disebut sumbu f(x). Jika fungsi di atas dituliskan dalam bentuk y = 2x + 1, maka sumbu tegak disebut sumbu y. Jadi, y = f(x).
Grafik fungsi f(x) = 2x + 1 atau y = 2x + 1 berupa garis lurus, maka bentuk y = 2x + 1 disebut persamaan garis lurus. Adapun sifat-sifat persamaan garis lurus adalah sebagai berikut:
1. Garis Sejajar
2. Garis Berimpit
3. Garis Tegak Lurus
4. Garis Berpotongan
Rumus Persamaan Garis Lurus
Rumus persamaan garis lurus dinyatakan dalam dua bentuk yaitu bentuk eksplisit dan bentuk implisit, apa itu?
Bentuk Eksplisit adalah bentuk persamaan garis lurus dituliskan dengan y = mx + c dimana x dan y merupakan variabel sedangkan m dan c adalah konstanta. Dalam hal ini, m sering disebut koefisien arah atau gradien dari garis lurus. Sehingga untuk garis yang persamaannya y = 2x + 1 dengan gradien m = 2.
Bentuk implisit dimana persamaan y = 2x + 1 dapat diubah ke bentuk lain yaitu 2 x - y + 1 = 0. Jadi, bentuk umum lain dari persamaan garis lurus dituliskan dengan Ax + By + C = 0.
Sementara itu, untuk mencari persamaan garis lurus sendiri terdapat dua cara. Pertama jika gradiennya diketahui dan garis melalui satu titik, kedua jika diketahui dua titik yang dilalui garis. Berikut rumus persamaan garis lurus:
1. Diketahui gradien dan satu titik yang dilalui garis, maka y - y1 = m (x-x1)
2. Diketahui dua titik yang dilalui garis, maka:
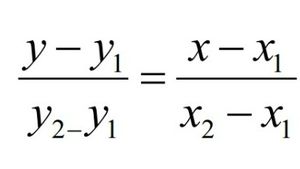 Rumus persamaan garis lurus. Foto: Modul Persamaan Garis Lurus yang disusun oleh Atmini Dhoruri Rumus persamaan garis lurus. Foto: Modul Persamaan Garis Lurus yang disusun oleh Atmini Dhoruri |
Contoh Soal Persamaan Garis Lurus dan Pembahasannya
Contoh soal 1
 Contoh soal persamaan garis lurus dan pembahasannya. Foto: Modul Persamaan Garis Lurus yang disusun oleh Atmini Dhoruri Contoh soal persamaan garis lurus dan pembahasannya. Foto: Modul Persamaan Garis Lurus yang disusun oleh Atmini Dhoruri |
Contoh soal 2
 Contoh soal persamaan garis lurus dan pembahasannya. Foto: Modul Persamaan Garis Lurus yang disusun oleh Atmini Dhoruri Contoh soal persamaan garis lurus dan pembahasannya. Foto: Modul Persamaan Garis Lurus yang disusun oleh Atmini Dhoruri |
Nah, untuk menentukan persamaan garis lurus ternyata mudah bukan detikers? Semoga membantu, ya!
(kri/kri)