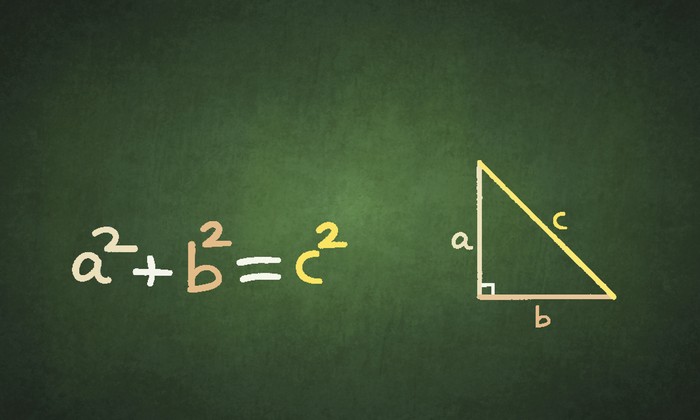Teorema Pythagoras: Sejarah, Bunyi, Rumus, Contoh Soal, dan Pembahasan

Rumus Pythagoras — Foto: Getty Images/iStockphoto/desifoto/Teorema Pythagoras: Sejarah, Bunyi, Rumus, Contoh Soal, dan Pembahasan

Jakarta -

Pythagoras (582 SM-496 SM) lahir di Pulau Samos, Yunani Selatan. Salah satu peninggalannya yang paling populer adalah teorema pythagoras.

Berdasarkan sejarah, isi teorema pythagoras sebetulnya sudah diketahui dan diterapkan orang-orang Babilonia dan India berabad-abad sebelum lahirnya Pythagoras. Namun, teorema itu dianggap sebagai penemuan Pythagoras karena dialah yang pertama membuktikan pengamatan tersebut secara matematis.

Pythagoras juga menemukan hal penting lainnya dalam bidang matematika, yaitu rasio emas atau golden ratio. Pada masa lalu, matematika tidak hanya berkaitan dengan bilangan, melainkan juga untuk menjabarkan filsafat dan memahami keindahan.

Selain itu, ada pula benda-benda yang disebut mengarah pada rasio emas, misalnya cangkang siput, galur-galur pada nanas, dan ukuran tubuh bagian atas manusia dibandingkan bawahnya. Seluruhnya mendekati rasio emas 1: 1,618.

Disebutkan dalam Menerabas Belantara Pythagoras karya Tugino, Pythagoras membuktikan, semua benda yang memenuhi rasio emas senantiasa mempunyai tingkat estetika sangat tinggi.

Bunyi Teorema Pythagoras

Teorema Pythagoras, sebagaimana dikutip dari buku Super Complete Rumus Matematika IPA SMP/MTs 7, 8, 9 oleh Elis Khoerunnisa dna Arinta Dra Setiana berbunyi, "Pada segitiga siku-siku, kuadrat panjang sisi miring (hipotenusa) adalah sama dengan jumlah kuadrat sisi-sisi penyikunya."

Hubungan antar sisi panjang segitiga siku-siku adalah sebagai berikut:

1. AC2 = AB2 + BC2 atau c2 = a2 + b2

2. AB2 = AC2 - BC2 atau a2 = c2 - b2

3. BC2 = AC2 - AB2 atau b2 = c2 - a2

Rumus Pythagoras

Rumus pythagoras adalah sebagai berikut:

a2 + b2 = c2

Keterangan:

c = sisi miring
a = tinggi
b = alas

Tripel Pythagoras

Tripel pythagoras adalah bilangan-bilangan yang membentuk segitiga siku-siku. Bilangan tersebut juga berlaku kelipatan. Berikut ini beberapa tripel pythagoras:

3, 4, 5 dan kelipatannya, (5 = sisi miring)
5, 12, 13 dan kelipatannya, (13 = sisi miring)
8, 15, 17 dan kelipatannya, (17 = sisi miring)
7, 24, 25 dan kelipatannya, (25 = sisi miring)
20, 21, 29 dan kelipatannya, (29 = sisi miring)
9, 40, 41 dan kelipatannya, (41 = sisi miring)
11, 60, 61 dan kelipatannya, (61 = sisi miring)

Contoh Soal Pythagoras dan Pembahasannya

Mengutip Buku Siswa Matematika untuk SMP/MTs Kelas VIII oleh Agus Supriyanto dan Miftahudin, teorema pythagoras dapat digunakan untuk memecahkan berbagai soal dalam matematika, utamanya yang berhubungan dengan bangun datar dan bangun ruang. Ini dia contoh soal pythagoras:

1. Panjang kedua sisi siku-siku sebuah segitiga adalah 9 cm dan 12 cm. Hitunglah panjang hipotenusa (sisi miring) segitiga tersebut!

Cara mengerjakan:

Panjang kedua sisi siku-siku tersebut misalnya a dan b. Hipotenusa atau sisi miring segitiga tersebut misalnya c.

Jika diketahui a = 9cm dan b = 12cm, maka menurut teorema pythagoras berlaku:

c2 = a2 + b2

c2 = (9 cm)2 + (12 cm)2

c2 = 81 cm2 + 144 cm2

c2 = 225 cm2

c = 15 cm

Maka, panjang hipotenusa segitiga siku-siku tersebut adalah 15 cm.

Mengutip arsip detikEdu, berikut ini contoh lain soal teorema pythagoras:

2. Terdapat segitiga EFG dengan siku-siku di Q. Apabila panjang sisi EF adalah 5 cm dan FG adalah 12 cm, maka berapa panjang EG?