Tabel Sudut Istimewa Trigonometri Berikut Contoh Soalnya

Apa itu sudut istimewa? Dalam Modul Matematika Umum Kelas X dalam materi Rasio Trigonometri, sudut istimewa adalah sudut tertentu yang nilai perbandingan trigonometrinya dapat dicari tanpa memakai perhitungan atau kalkulator.

Dengan kata lain, sudut istimewa trigonometri secara langsung mengungkap rasio panjang sisi pada sudut tertentu. Adapun sudut istimewa diantaranya yaitu sudut 0°, 30°, 45°, 60°, dan 90°.

Trigonometri dalam ilmu matematika mempelajari sudut, sisi, hingga perbandingan antara sudut dan sisi khususnya pada segitiga siku-siku dengan menggunakan sin, cos, tan, dan lainnya.

Perbandingan Sudut Istimewa Trigonometri

Dalam Modul Matematika Umum yang disusun oleh Entis Sutisna (2020), dapat kita ketahui hubungan trigonometri dengan sudut-sudut istimewa di atas dengan tabel sin cos tan sebagai berikut:

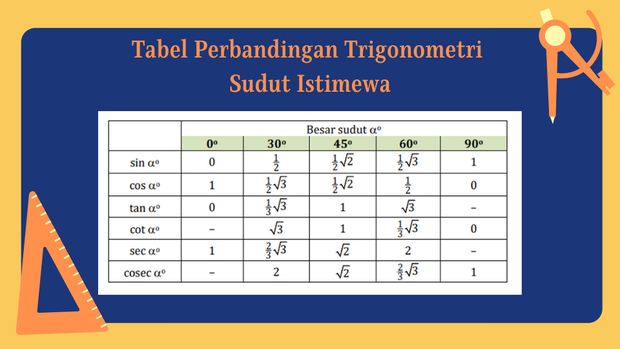Tabel perbandingan trigonometri sudut istimewa Foto: detikEdu

Dari tabel perbandingan trigonometri sudut istimewa di atas, dapat kita ketahui bahwa:

• tan α = sin α / cos α
• sec α = 1 / cos α
• cosec α = 1 / sin α
• cotan α = 1 / tan α

Contoh Soal Sudut Istimewa

1. Hitunglah tan 30° + tan 45 °

Jawab:

tan 30° + tan 45° = 1/3 √3 + 1 = 1/3 (√3 + 3)

2. Tunjukkan bahwa sin2 45o + cos2 45o = 1

Jawab:

sin2 45o + cos2 45o = (1/2 √2)2 + (1/2 √2)2 = ½ + ½ = 1

Identitas Trigonometri

Perlu kita ketahui, identitas trigonometri adalah hubungan suatu fungsi trigonometri dengan fungsi trigonometri lainnya sehingga menimbulkan kesamaan perbandingan dari suatu sudut.

Terdapat 3 cara untuk menunjukkan kebenaran identitas trigonometri yaitu sebagai berikut:

Cara 1 yaitu sederhanakan ruas kiri dengan identitas sebelumnya hingga menjadi bentuk yang sama dengan ruas kanan.

Cara 2 yaitu mengubah ruas kanan hingga menjadi bentuk yang sama dengan ruas kiri.

Cara 3 yaitu mengubah ruas kiri maupun kanan ke dalam bentuk yang sama.

Berikut ini merupakan rumus identitas trigonometri yang perlu kamu ketahui:

• tan α = sin α / cos α
• cot α = cos α / sin α = 1 / tan α
• sec α = 1 / cos α
• csc α = 1 / sin α
• sin2 x + cos2 x = 1
• sin2 x = 1 - cos2 x
• cos2 x = 1 - sin2 x
• sec2 α = tan2 α + 1
• csc2 α = cot2 α + 1

Setelah mengetahui tabel sudut istimewa dan memahami contoh soal di atas, tahukah kamu kegunaan perhitungan trigonometri dalam kehidupan kita?

Contoh penerapan trigonometri yaitu misalnya menghitung tinggi bangunan, gunung, pohon dan lainnya. Pada bidang astronomi, trigonometri digunakan untuk navigasi di laut, udara, bahkan angkasa. Trigonometri juga berguna dalam teori musik akustik, optik, dan lainnya.

Selain itu, dalam bidang teknik sipil rumus-rumus di atas termasuk sudut sudut istimewa trigonometri dapat membantu pengukuran tanah guna menentukan posisi ruang tiga dimensi dari suatu tempat di permukaan bumi. Misalnya membuat peta topografi bumi untuk menentukan luas wilayah tertentu.

Video Trump Sebut Mahasiswa Tak Bisa Hitung 2+2 tapi Malah ke Harvard

Video Trump Sebut Mahasiswa Tak Bisa Hitung 2+2 tapi Malah ke Harvard