Contoh soal PAS matematika kelas 11 semester 2 Kurikulum Merdeka bisa dijadikan bahan belajar bagi siswa menjelang penilaian akhir semester (PAS).
Menghadapi waktu PAS, siswa bisa membaca kembali materi yang pernah dipelajari. Namun, untuk mempertajam analisis pemahaman siswa bisa berlatih contoh soal.
Oleh karena itu, berikut contoh soal PAS matematika kelas 11 semester 2 dikutip dari buku Matematika SMA/MA/SMK/MAK Kelas XI oleh Sudianto Manullang dkk:
SCROLL TO CONTINUE WITH CONTENT
Contoh Soal PAS Matematika Kelas 11 Semester 2
1. Buktikan dengan induksi matematika bahwa jumlah n bilangan ganjil positif yang pertama sama dengan n²!
Jawaban dan pembahasan:
- Untuk n = 1, maka P(1) = 1 = 1² = 1. Jadi P(1) benar
- Karena P(1) benar, maka P(2) juga benar, hingga dapat diperoleh untuk n = k
- P(k) = 1 + 3 + 5 + 7 + . . . + (2k - 1) = k² juga benar, untuk setiap k bilangan asli.
- Akan ditunjukkan untuk bahwa untuk n = k + 1, sedemikian sehingga
P(k + 1) = 1 + 3 + 5 + 7 + . . . + (2(k + 1) - 1) = (k + 1)² adalah suatu pernyataan yang benar
- Karena P(k) = 1 + 3 + 5 + 7 + . . . + (2k - 1) = k² adalah pernyataan yang benar, maka 1 + 3 + 5 + 7 + . . . + (2k - 1) = k²
- Jika kedua ruas ditambahkan dengan (2k + 1), akibatnya 1 + 3 + 5 + 7 + . . . + (2k - 1) + (2k + 1) = k²+ 2k + 1 = (k + 1)²
Jadi, dengan P(k) ditemukan P(k + 1). Dengan demikian terbukti bahwa: 1 + 3 + 5 + 7 + . . . + (2n - 1) = n² adalah benar, untuk setiap n bilangan asli.
2. Gambarkan daerah penyelesaian sistem pertidaksamaan berikut ini!
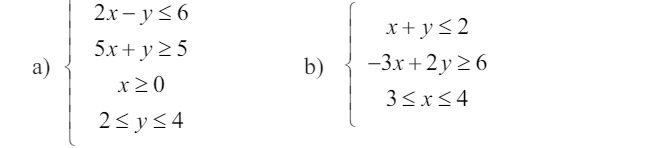 |
Jawaban dan pembahasan:
Untuk menggambarkan daerah penyelesaian setiap pertidaksamaan pada sistem di atas, dapat dimulai dengan menggambar satu per satu pertidaksamaan yang diketahui. Tentu, semua daerah penyelesaian tersebut nanti harus disajikan dalam satu bidang koordinat kartesius.
a. Daerah penyelesaian untuk sistem pertidaksamaan (a) di atas, adalah sebagai berikut
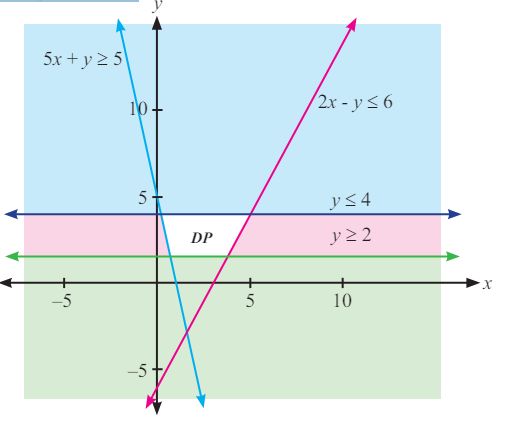 |
b. Daerah penyelesaian untuk sistempertidaksamaan (b) di atas, adalah sebagai berikut:
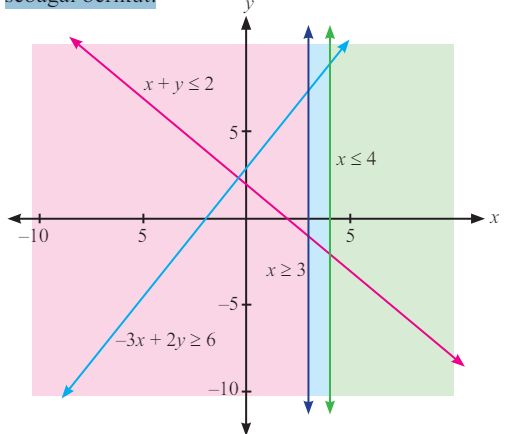 |
Jadi, tidak ada nilai x dan y yang memenuhi sistempertidaksamaan b. Hal ini, perlu dicatat, bahwa tidak semua masalah memiliki penyelesaian.
3. Seorang wisatawan lokal hendak berlibur ke beberapa tempat wisata yang ada di Pulau Jawa. Untuk memaksimalkan waktu liburan, dia mencatat jarak antara kota-kota tersebut sebagai berikut.
Bandung - Semarang 367 km
Semarang - Yogyakarta 115 km
Bandung - Yogyakarta 428 km
Buatlah susunan jarak antar kota tujuan wisata tersebut jika wisatawan tersebut memulai perjalanannya dari Bandung!
Jawaban dan pembahasan:
Wisatawan akan memulai perjalanannya dari Bandung ke kota-kota wisata di Pulau Jawa. Jarak antar kota tujuan wisata dituliskan sebagai berikut.
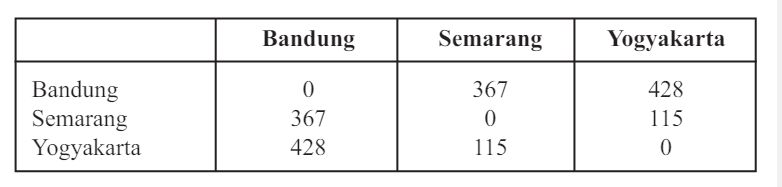 |
Berdasarkan tampilan di atas, dapat dilihat jarak antar kota tujuan wisata dengan membaca data dari baris ke kolom. Susunan tersebut dapat juga
dituliskan sebagai berikut.
 |
Susunan jarak antar kota di Pulau Jawa ini terdiri dari 3 baris dan 3 kolom.
4. Tentukanlah nilai a, b, c, dan d yang memenuhi matriks Pt = Q, dengan
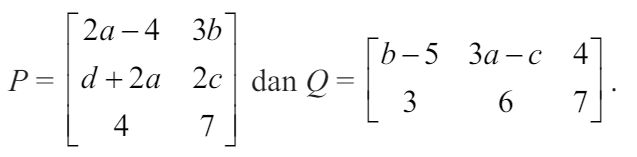 |
Jawaban dan pembahasan:
Karena P merupakan matriks berordo 2 × 3, maka Pt merupakan matriks berordo 2 × 3. Matriks Q merupakan matriks berordo 2 × 3. Oleh karena itu berlaku kesamaan matriks Pt = Q
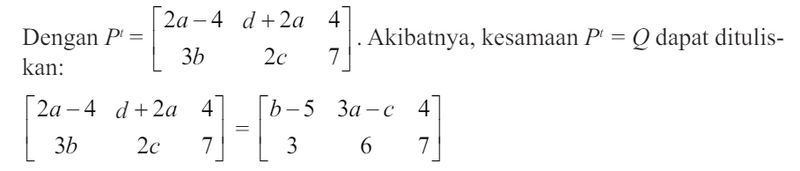 |
Dari kesamaan di atas, kita temukan nilai a, b, c, dan d sebagai berikut.
• 3b = 3 maka b = 1, dan 2c = 6 maka c = 3.
• 2a - 4 = -4 maka a = 0.
• Karena a = 0 maka d = -3.
Jadi, a = 0, b = 1, c = 3, dan d = -3.
5. Sebuah pabrik tekstil hendak menyusun tabel aktiva mesin dan penyusutan mesin selama 1 tahun yang dinilai sama dengan 10% dari harga perolehan sebagai berikut:
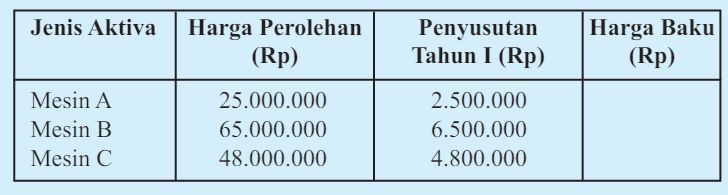 |
Lengkapilah tabel tersebut dengan menggunakan matriks!
Jawaban dan pembahasan:
 |
Misalkan A dan B adalah matriks-matriks berordo m × n. Pengurangan matriks A dengan matriks B didefinisikan sebagai jumlah antara matriks A
dengan matriks -B. Ingat, Matriks -B adalah lawan dari matriks B. Ditulis:
A - B = A + (-B).
Matriks dalam kurung merupakan matriks yang entrynya berlawanan dengan setiap entry yang bersesuaian matriks B
6. Titik A(1, 4) dicerminkan terhadap titik asal O(0, 0), tentukan bayangan A!
Jawaban dan pembahasan:
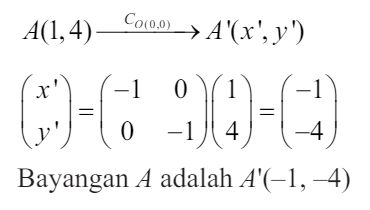 |
7. Sebuah garis dengan persamaan -2x + 4y - 1 = 0 dicerminkan terhadap titik asal O(0, 0). Tentukan persamaan bayangan garis tersebut!
Jawaban dan pembahasan:
Misalkan titik A(x, y) memenuhi persamaan -2x + 4y - 1 = 0 sedemikian
sehingga:
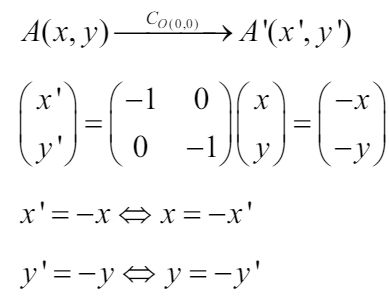 |
Jika x dan y disubstitusi ke garis maka ditemukan bayangannya yaitu:
-2(-x) + 4(-y) -1 = 0 atau 2x - 4y - 1 = 0
8. Ibu Depi membeli sebuah sepeda motor dari dealer yang menggunakan sistem anuitas pada pembayaran kreditnya. Harga motor tersebut adalah Rp10.000.000,00 dengan menggunakan tingkat suku bunga 4% per tahun. Ibu Depi berencana melunaskan kreditnya dengan 6 kali anuitas. Hitunglah besar anuitas yang dibayarkan oleh Ibu Depi?
Jawaban dan pembahasan:
M = Rp10.000.000,00 ; i = 4% = 0,04 ; n = 6
Maka besar anuitasnya:
 |
Maka besar anuitas yang dibayarkan tiap pembayarannya sebesar Rp1.907.619,00.
9. Jika f(x) = x² - 4x maka tentukan nilai pendekatan f(x) pada saat x mendekati 1
Jawaban dan pembahasan:
 |
10. Tentukan turunan f(x) = (2x² - 3x)⁴
Jawaban dan pembahasan:
Misalkan u(x) = 2x²- 3x sehingga u'(x) = 4x - 3
Dengan demikian f(x) = (2x²- 3x)⁴ menjadi f(x) = (u(x))⁴ sehingga
f '(x) = 4(u(x))3u'(x).
Jadi, f '(x) = 4(2x² - 3x)³(4x - 3) atau f '(x) = 4(4x - 3)(2x² - 3x)³
.
Demikian latihan soal PAS matematika kelas 11 semester 2 Kurikulum Merdeka beserta jawaban dan pembahasannya. Semoga bermanfaat ya.
(cyu/nwk)


























































