10 Contoh Soal UTBK-SNBT 2024 Penalaran Matematika, Ada Pembahasannya!

Ilustrasi belajar — Yuk belajar 10 cotoh soal UTBK SNBT 2024 Penalaran Matematika berikut ini! Foto: Getty Images/PrathanChorruangsak

Jakarta -

Subtes penalaran matematika bertujuan mengukur kemampuan berpikir menggunakan konsep, prosedur, fakta, dan alat matematika untuk menyelesaikan masalah sehari-hari. Berbagai komponen soal yang diujikan telah kamu pelajari sejak jenjang SMP hingga SMA.

Dari materi baris bilangan, himpunan dan diagram venn, aritmetika sosial, pencacahan dan peluang, hingga geometri tentang sudut dan bangun datar.

Siap kembali mengulasnya? Berikut 10 contoh soal UTBK-SNBT 2024 dikutip dari buku Top Rank SNBT 2024 karya Tim Bintang Nusantara.

SCROLL TO CONTINUE WITH CONTENT

10 Contoh Soal UTBK-SNBT 2024 Penalaran Matematika

1. Barisan 16, p, 4, q, ..... merupakan barisan aritmetika. Jumlah suku ke-6 dan suku ke-8 barisan tersebut sama dengan hasil kali suku ke-4 yakni.....

A. 2
B. 4
C. 8
D. 14
E. 20

Jawaban: E. 20
Pembahasan:
Barisan aritmetika:
16, p, 4, q, .....
U3 = 4
a + (n-1)b = 4
16 + 2b = 4
2b = -12
b = -6

Maka:
U6 + U8 = x . U4
a + 5b + a + 7b = x(a + 3b)
2a + 12b = x(a + 3b)
2(16) + 12(-6) = x(16 + 3(-6))
32-72 = -2x
-40 = -2x
-40/-2 = x
20 = x

2. Barisan 1, 2, y .... merupakan barisan geometri. Nilai 6 - y adalah.....

A. 2
B. 1
C. 0
D. -1
E. -2

Jawaban: A. 2
Pembahasan:
1, 2, y, ..... merupakan barisan geometri.

Rasionya: R = U2/U1 = 2/1 = 2
y = U3 = ar^2 = 1.2^2 = 4
Maka nilai 6 - y = 6 - 4 = 2

3. Diketahui diagram Venn sebagai berikut:

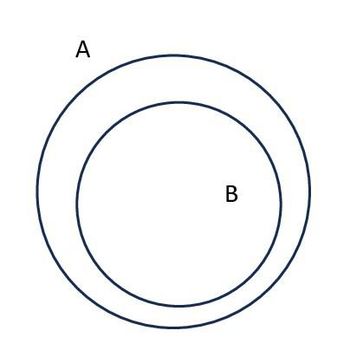Soal UTBK-SNBT 2024 Penalaran Matematika Foto: dok. Bank Soal

Pasangan himpunan yang memiliki diagram venn seperti di atas adalah.....

A.
A = Himpunan hewan bertulang belakang
B = Himpunan hewan yang dapat terbang

B.
A = Himpunan bilangan bulat positif
B = Himpunan bilangan bulat negatif

C.
A = Himpunan bilangan prima
B = Himpunan bilangan genap

D.
A = Himpunan bayi
B = Himpunan orang dewasa

E.
A = Himpunan ibu kota provinsi
B = Himpunan negara-negara ASEAN

Jawaban: A.
A = Himpunan hewan bertulang belakang
B = Himpunan hewan yang dapat terbang
Pembahasan:
Pasangan himpunan yang tepat adalah seluruh elemen dalam himpunan B terdapat pada himpunan A, jadi yang sesuai adalah jawaban A.

4. Kakak diberi uang sebesar n oleh ayah. Uang tersebut digunakan untuk membeli buku 0,2 bagian, membeli tempat pensil 0,12 bagian, membeli makanan 0,28 bagian dan membeli kaos kaki sebesar Rp 15.000,00. Uang yang masih dimiliki kakak akan ditabung di sekolah seluruhnya. Besar uang kakak yang akan ditabung adalah....

A. 0,4n - Rp 15.000,00
B. 0,4n + Rp 15.000,00
C. 0,6n - Rp 15.000,00
D. 0,6n + Rp 15.000,00
E. 0,2n - Rp 15.000,00

Jawaban: A. 0,4n - Rp 15.000,00
Pembahasan:
Jumlah yang dari ayah = n
Bagian untuk membeli buku = 0,2
Bagian untuk membeli tempat pensil = 0,12
Bagian untuk membeli makanan = 0,28
Uang untuk membeli kaos kaki = Rp 15.000
Uang yang ditabung adalah:
= (1 - 0,2 - 0,12 - 0,28)n - Rp 15.000
= 0,4n - Rp 15.000

5. Sebanyak 1.000 petani akan menanam jenis bunga. Ada 900 orang menanam bunga mawar dan 500 orang menanam bunga melati. Jika x adalah jumlah minimum petani menanam keduanya dan y adalah jumlah maksimum petani menanam kedua-keduanya maka nilai x+y = ....

A. 1.000
B. 900
C. 800
D. 700
E. 400

Jawaban: B. 900
Pembahasan:
Nilai x = Dari data angka penanam bunga melati menjadi minimum yakni 500 orang. Sehingga jumlah petani yang hanya menanam bunga mawar = 900-500 = 400

Nilai y = 900 + 500 - 1000 = 400
Jadi, x + y = 500 + 400 = 900

6. Bobi memiliki kertas bernomor 6 sampai 13. Bobi akan mengambil 1 kertas saat pengambilan pertama, kertas tidak dikembalikan. Ia mengambil lagi satu kertas secara acak. Peluang Bobi mendapatkan kertas bernomor ganjil pada pengambilan pertama dan genap pada pengambilan kedua adalah.....

A. 1/7
B. 2/7
C. 3/7
D. 5/7
E. 6/7

Jawaban: B. 2/7
Pembahasan:
Nomor kertas = 6, 7, 8, 9, 10, 11, 12, 14
Nomor kertas genap = 6, 8, 10, 12
Nomor kertas ganjil = 7, 9, 11, 13

Peluang Bobi mendapat kertas bernomor ganjil pada pengambilan pertama dan genap pada pengambilan kedua adalah: 4/8 x 4/7 = 16/56 = 2/7

7. Kurva y = x^2 + 6x -27 dan garis y = x + n akan bersinggungan. Nilai n adalah.....

A. -33 1/4
B. -33 2/4
C. -33 3/4
D. 33 3/4
E. 33 1/4

Jawaban: A. -33 1/4
Pembahasan:
y = y
x^2 + 6x - 27 = x+n
x^2 + 6x - x - 27 - n = 0
x^2 + 5x - 27 -n = 0

Syarat bersingungan adalah D = 0
D = b^2 - 4ac
0 = 5^2 - 4.1(-27-n)
0 = 25 + 108 + 4n
0 = 133 + 4n
-4n = 133
n = 133/-4 = -33 1/4

8. Diketahui x dan y merupakan bilangan ganjil. Manakah yang merupakan bilangan genap?

(1) x + y
(2) 3x + 2y
(3) 3x - 9y
(4) 3x - 2y

A. 1, 2, dan 3 benar
B. 1 dan 3 benar
C. 2 dan 4 benar
D. Hanya 4 yang benar
E. Semua pilihan benar

Jawaban: B. 1 dan 3 benar
Pembahasan:
- Bilangan ganjil jika dikalikan dengan bilangan ganjil akan menghasilkan bilangan ganjil.
- Bilangan ganjil jika dikalikan dengan bilangan genap akan menghasilkan bilangan genap.
- Bilangan ganjil jika ditambahkan dengan bilangan ganjil akan menghasilkan bilangan genap sebaliknya jika bilangan ganjil ditambah bilangan genap akan menghasilkan bilangan ganjil.
- Bilangan ganjil jika dikurangkan dengan bilangan ganjil akan menghasilkan bilangan ganjil, sebaliknya jika bilangan ganjil dikurangkan bilangan ganjil akan menghasilkan bilangan genap.

Jadi, jika x dan y adalah bilangan ganjil operasi yang menghasil bilangan genap maka jawaban yang tepat adalah x + y dan 3x - 9y.

9. Perhatikan gambar berikut!

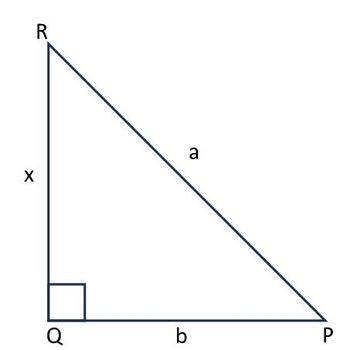Soal UTBK-SNBT 2024 Penalaran Matematika Foto: dok. Bank Soal

Tentukan nilai x!

(1) < P = 30°
(2) a = 18 cm

A. Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup
B. Pernyataan (2) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (1) SAJA tidak cukup
C. DUA pernyataan BERSAMA-SAMA cukup untuk menjawab pertanyaan, tetapi SATU pernyataan SAJA tidak cukup
D. Pernyataan (1) SAJA cukup untuk menjawab pertanyaan dan pernyataan (2) SAJA cukup
E. Pernyataan (1) dan pernyataan (2) tidak cukup untuk menjawab pertanyaan

Jawaban: C. DUA pernyataan BERSAMA-SAMA cukup untuk menjawab pertanyaan, tetapi SATU pernyataan SAJA tidak cukup
Pembahasan:

(1) pernyataan satu benar.
(2) Jika a = 18 dan misalkan b= x√3 maka a= 2x
a = 18
2x = 19
x = 9

Jadi, jawaban paling tepat adalah C.

10. Sebuah lingkaran memiliki keliling 220 cm. Luas temberengnya adalah....

(1) π = 22/7
(2) π = 3,14

Jawaban: E. Pernyataan (1) dan pernyataan (2) tidak cukup untuk menjawab pertanyaan
Pembahasan:
Dengan diketahui keliling lingkaran, maka luas tembereng dapat dicari jika ada sudut pusat yang ada di hadapan busur yang membatasinya. Jadi, jawaban paling tepat E.

Nah itulah 10 contoh soal Penalaran Matematika untuk UTBK-SNBT 2024. Selamat berlatih detikers!