Mari Belajar Barisan Geometri, Ketahui Rumus dan Contoh Soal

Detikers, belajar matematika di sekolah pasti mengenal apa itu barisan kan?

Barisan adalah konsep matematika yang sering digunakan untuk menganalisis pola dan urutan angka. Barisan merujuk pada suatu urutan bilangan atau kumpulan angka dengan elemen yang diatur dalam urutan tertentu. Elemen-elemen ini dapat dihitung berdasarkan aturan tertentu.

Adapun jenis barisan ada bermacam-macam, sesuai dengan aturan dari suku satu ke suku lainnya. Ada barisan aritmatika, barisan geometri, hingga barisan prima. Salah satu jenis barisan yang menarik dan penting adalah barisan geometri.

Mengutip dari buku Mudah dan Aktif Belajar Matematika ditulis oleh Tri Dewi Listya, barisan geometri adalah suatu barisan bilangan yang hasil bagi dua suku atau angka yang berurutan akan selalu tetap (sama).

Perbandingan dua suku angka yang berurutan pada barisan geometri akan selalu sama. Hasil perbandingan tersebut dikenal dengan rasio yang dilambangkan dengan r. Dengan r tertentu, kita bisa menemukan suku/angka ke-n dalam suatu barisan geometri.

Rumus Barisan Geometri

Menurut Modul Pembelajaran SMA Matematika Kelas XI, rasio dari barisan geometri dapat dihitung menggunakan rumus berikut:

Rumus rasio barisan geometri Foto: dok. Kemdikbud

Keterangan:

U1 : suku ke-1

U2 : suku ke-2

U3 : suku ke-3

U4 : suku ke-4

Bila rasio sudah diketahui, maka mencari suku ke-n akan lebih mudah. Rumus mencari suku ke-n dalam barisan geometri sebagai berikut:

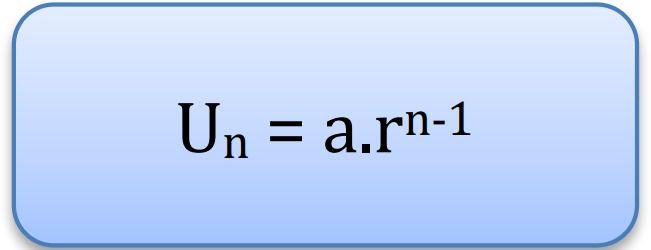Rumus suku ke-n barisan geometri Foto: dok. Kemdikbud

Keterangan:

Un : suku ke-n

a : suku pertama

r : rasio

n : angka urutan suku ke-

Contoh Soal Barisan Geometri dan Pembahasannya

Soal 1

Diberikan suatu barisan 3, 9, 27, 81... Diketahui barisan tersebut merupakan barisan geometri. Tentukan suku ke-5 dari barisan tersebut.

Pembahasan 1

Seperti yang kita ketahui, barisan geometri memiliki rasio konstan antara dua suku berurutan. Oleh karena itu, kita cari rasio dari barisan tersebut lebih dulu.

r = u2/ u1 = 9/3

= 3

Setelah mengetahui bahwa rasio tersebut adalah 3 maka kita masukkan dalam rumus suku ke-n

U5 = 3 x 3 (5-1)

= 3 x 3(4)

= 3 x 81

= 243

Jadi, suku ke-5 dari barisan geometri tersebut adalah 243

Soal 2

Diberikan barisan geometri pecahan sebagai berikut : 1/2, 1/4, 1/8, 1/16,..... Tentukan suku ke-6 dalam barisan tersebut.

Pembahasan 2

Dalam barisan geometri dengan angka pecahan, kita juga dapat menggunakan rumus umum barisan geometri untuk mencari suku ke-n. Rumus tersebut tetap berlaku, hanya saja kita harus memahami bagaimana mengaplikasikannya pada angka pecahan.

Diketahui:

a1 = ½ dan a2 = 1/4

Maka rasio barisan tersebut adalah 1/4 : 1/2 = ½

Sekarang kita bisa menggunakan rumus ini untuk mencari suku ke-6 setelah mengetahui bahwa rasio barisan tersebut adalah 1/2.

U6 = 1/2 x (½ (6-1))

U6 = 1/2 x (½ (5))

U6 = 1/2 x 1/32

U6 = 1/64

Jadi, suku ke-6 dalam barisan geometri tersebut adalah 1/64

Video Trump Sebut Mahasiswa Tak Bisa Hitung 2+2 tapi Malah ke Harvard

Video Trump Sebut Mahasiswa Tak Bisa Hitung 2+2 tapi Malah ke Harvard