7 Contoh Penerapan Statistika Deskriptif dalam Berbagai Bidang

Statistika deskriptif merupakan salah satu cabang ilmu statistika yang banyak digunakan dalam kehidupan sehari-hari. Agar lebih paham, berikut contoh-contoh penerapan statistika deskriptif dalam berbagai bidang.

Mengutip dari Jurnal Universitas Pamulang, statistika deskriptif adalah metode statistika untuk mengumpulkan, menyusun, mengolah, menyajikan dan menganalisis data angka. Hal ini digunakan untuk memberikan gambaran yang teratur, ringkas, dan jelas mengenai suatu kondisi.

Dengan statistika deskriptif kita bisa merangkum dan menginterpretasikan data sehingga mudah dipahami. Selanjutnya dari situ kita dapat menarik pengertian ataupun makna tertentu.

Statistika deskriptif ini dapat digunakan dalam berbagai bidang seperti ekonomi, bisnis, pendidikan, kesehatan, olahraga, demografi kependudukan, pariwisata dan lain sebagainya.

Nah untuk lebih jelasnya, berikut beberapa contoh statistika deskriptif dalam berbagai bidang yang dihimpun detikSulsel dari berbagai sumber. Yuk disimak!

Contoh Statistika Deskriptif

Melalui statistika deskriptif kita bisa mengetahui beberapa nilai dari sebuah dataset. Di antaranya, mean (nilai rata-rata), median, modus, rentang (range) dan lain sebagainya.

Contoh penggunaan statistika deskriptif dalam kehidupan sehari-hari adalah penghitungan Indeks Prestasi Kumulatif (IPK) mahasiswa, di mana pihak kampus mengumpulkan poin data dari berbagai nilai, kelas, dan ujian untuk mengetahui IPK.

Statistika deskriptif juga sering digunakan dalam bisnis untuk menganalisis penjualan, seperti menghitung rata-rata penjualan harian atau menentukan produk mana yang paling sering terjual.

Untuk lebih jelasnya, berikut contoh kasus perhitungannya dalam kehidupan sehari-hari.

1. Contoh Penerapan Statistika Deskriptif di Dunia Pendidikan

Dalam dunia pendidikan, kita bisa menghitung rata-rata nilai ujian siswa di sebuah kelas untuk menentukan kinerja keseluruhan kelas tersebut.

a. Mean (Rata-rata):

Sebuah kelas memiliki nilai ujian sebagai berikut: 70, 75, 80, 65, dan 90.

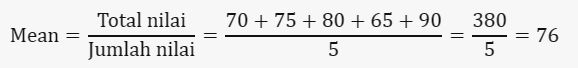Contoh statitistika deskriptif Foto: Edward R/detikSulsel

b. Median:

Nilai ujian dari kelas yang sama setelah diurutkan: 65, 70, 75, 80, 90.

Median adalah nilai tengah, jadi median = 75.

c. Modus:

Frekuensi kemunculan nilai ujian: 70, 75, 75, 80, 90.

Modus adalah nilai yang paling sering muncul, jadi modus = 75.

d. Rentang (Range):

Nilai tertinggi adalah 90 dan nilai terendah adalah 65.

Range = Nilai tertinggi - Nilai terendah = 90-65 = 25

e. Kuartil:

Untuk menentukan kuartil, data harus diurutkan: 65, 70, 75, 80, 90.

Kuartil kedua (Q2) adalah median = 75. Kuartil pertama (Q1) adalah median dari separuh pertama data = 70. Kuartil ketiga (Q3) adalah median dari separuh kedua data = 80.

f. Desil:

Desil ke-5 dari data yang sama akan menjadi nilai tengah dari data yang telah diurutkan, yaitu 75.

g. Persentil:

Persentil ke-50 dari data yang sama juga akan menjadi nilai tengah, yaitu 75.

h. Standar Deviasi:

Menggunakan nilai ujian yang sama, pertama hitung mean = 76.

Kemudian hitung selisih kuadrat dari mean untuk setiap nilai:

(70-76)² + (75-76)² + (80-76)² + (65-76)² + (90 -76)² = 36+1+16+121+196

Rata-rata selisih kuadrat:

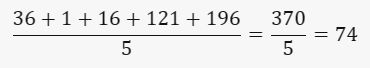contoh Foto: Edward R/detikSulsel

Standar deviasi adalah akar kuadrat dari rata-rata selisih kuadrat:

√74 = 8,6

i. Variansi:

Variansi adalah kuadrat dari standar deviasi, jadi:

Variasi = 8,6² = 73,96

j. Koefisien Variasi:

Koefisien variasi dihitung dengan membagi standar deviasi dengan mean:

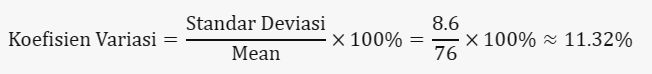contoh Foto: Edward R/detikSulsel

Ini adalah contoh sederhana untuk memahami bagaimana perhitungan statistika deskriptif dilakukan. Dalam prakteknya, data yang digunakan biasanya lebih kompleks dan banyak, sehingga memerlukan penggunaan software statistik untuk mempermudah perhitungan.

2. Contoh Statistika Deskriptif dalam Bidang Kesehatan

Kasus: Sebuah rumah sakit ingin menganalisis data tekanan darah pasien yang mengunjungi klinik hipertensi selama satu minggu.

Data Tekanan Darah (mmHg): 120, 125, 130, 128, 135, 140, 126

1. Mean (Rata-rata):

contoh Foto: Edward/detikSulsel

2. Median:

Data setelah diurutkan: 120, 125, 126, 128, 130, 135, 140.

Median adalah nilai tengah, jadi median = 128.

3. Modus:

Tidak ada nilai yang muncul lebih dari satu kali, sehingga tidak ada modus.

4. Rentang (Range):

Nilai tertinggi adalah 140 dan nilai terendah adalah 120.

Range = Nilai tertinggi - Nilai terendah = 140 - 120 = 20

5. Kuartil:

Kuartil kedua (Q2) adalah median = 128.
Kuartil pertama (Q1) adalah median dari separuh pertama data = 125.
Kuartil ketiga (Q3) adalah median dari separuh kedua data = 135.

6. Standar Deviasi:

Pertama, hitung mean = 129.14.
Kemudian hitung selisih kuadrat dari mean untuk setiap nilai:

(120-129.14)² + (125-129.14)² + ... + (140-129.14)²

Rata-rata selisih kuadrat:

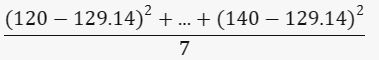contoh Foto: Edward/detikSulsel

Standar deviasi adalah akar kuadrat dari rata-rata selisih kuadrat:

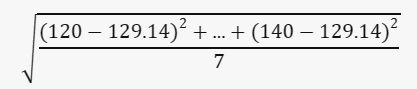contoh Foto: Edward/detikSulsel

7. Variansi:

Variansi adalah kuadrat dari standar deviasi.

8. Koefisien Variasi:

Koefisien variasi dihitung dengan membagi standar deviasi dengan mean:

Koefisien Variasi = Standar Deviasi/Mean X 100%

Perhitungan ini memberikan gambaran tentang distribusi tekanan darah pasien yang mengunjungi klinik. Dengan informasi ini, rumah sakit dapat mengevaluasi dan merencanakan intervensi yang sesuai untuk pasien dengan hipertensi.

3. Contoh Perhitungan Statistika Deskriptif dalam Dunia Bisnis

Kasus: Sebuah perusahaan ritel ingin menganalisis performa penjualan produknya selama satu bulan.

Data Penjualan Harian (dalam ribuan unit): 15, 20, 22, 18, 25, 30, 16, 19, 21, 23, 27, 29, 17, 14, 26

1. Mean (Rata-rata):

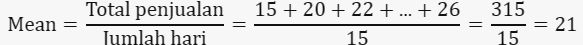contoh Foto: Edward/detikSulsel

2. Median:

Data setelah diurutkan: 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 25, 26, 27, 29, 30.
Median adalah nilai tengah, jadi median = 21.

3. Modus:

Tidak ada nilai yang muncul lebih dari satu kali, sehingga tidak ada modus.

4. Rentang (Range):

Nilai tertinggi adalah 30 dan nilai terendah adalah 14.

Range = Nilai tertinggi - Nilai terendah = 30 - 14 = 16

5. Kuartil:

Kuartil kedua (Q2) adalah median = 21.
Kuartil pertama (Q1) adalah median dari separuh pertama data = 17.
Kuartil ketiga (Q3) adalah median dari separuh kedua data = 26.

6. Standar Deviasi:

Pertama, hitung mean = 21.
Kemudian hitung selisih kuadrat dari mean untuk setiap nilai:

(15-21)² + (20-21)² +...+ (26-21)²

Rata-rata selisih kuadrat:

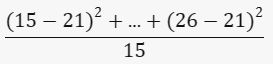contoh Foto: Edward R/detikSulsel

Standar deviasi adalah akar kuadrat dari rata-rata selisih kuadrat:

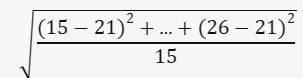contoh Foto: Edward R/detikSulsel

7. Variansi:

Variansi adalah kuadrat dari standar deviasi.

8. Koefisien Variasi:

Koefisien variasi dihitung dengan membagi standar deviasi dengan mean:

Koefisien Variasi = Standar Deviasi/Mean X 100%

Dengan menganalisis data ini, perusahaan dapat mengetahui hari-hari dengan penjualan tertinggi dan terendah, serta seberapa konsisten penjualan mereka dari hari ke hari. Informasi ini sangat berguna untuk membuat keputusan strategis seperti promosi, pengadaan stok, dan alokasi sumber daya.

4. Contoh Statistika Deskriptif dalam Dunia Olahraga

Untuk menghitung rata-rata skor permainan tim sepak bola selama satu musim, kita dapat menggunakan data skor yang dicetak dalam setiap pertandingan. Berikut adalah contoh kasus dan langkah-langkah perhitungannya:

Kasus: Tim sepak bola "A" telah memainkan 30 pertandingan dalam satu musim dan mencetak skor sebagai berikut (dalam jumlah gol per pertandingan): 2, 1, 3, 0, 4, 2, 1, 3, 2, 0, 1, 4, 3, 2, 1, 2, 3, 1, 0, 4, 2, 1, 3, 2, 0, 1, 4, 3, 2, 1.

1. Mengumpulkan Data:

Kita memiliki data skor untuk 30 pertandingan.

2. Menghitung Total Skor:

Menjumlahkan semua gol yang dicetak:

Total Skor = 2 + 1 + 3 + 0 + ... + 3 + 2 + 1 = 60

3. Menghitung Rata-rata Skor:

Membagi total skor dengan jumlah pertandingan:

Rata-rata Skor = Total Skor/Jumlah Pertandingan = 60/30 = 2

Dengan demikian, rata-rata skor per pertandingan untuk Tim "A" selama satu musim adalah 2 gol per pertandingan. Ini memberikan gambaran tentang efektivitas strategi ofensif tim. Jika tim ingin mengevaluasi strategi defensifnya, mereka juga bisa menghitung rata-rata gol yang kemasukan per pertandingan.

Analisis seperti ini membantu pelatih dan manajemen tim untuk menilai kinerja tim secara keseluruhan dan membuat keputusan strategis untuk peningkatan di masa depan.

5. Contoh Penerapan Statistika Deskriptif untuk Demografi Kependudukan

Kasus: Sebuah kota ingin menganalisis distribusi umur penduduknya untuk perencanaan layanan publik.

Data Umur Penduduk (dalam tahun): 5, 12, 17, 22, 22, 25, 29, 32, 32, 35, 37, 40, 42, 45, 50, 55, 60, 65, 70, 75

1. Mean (Rata-rata):

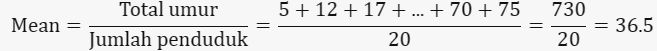contoh Foto: Edward R/detikSulsel

2. Median:

Data setelah diurutkan: 5, 12, 17, 22, 22, 25, 29, 32, 32, 35, 37, 40, 42, 45, 50, 55, 60, 65, 70, 75.

Median adalah nilai tengah, jadi median = 36.5.

3. Modus:

Nilai yang paling sering muncul adalah 22 dan 32, sehingga modus = 22 dan 32.

4. Rentang (Range):

Nilai tertinggi adalah 75 dan nilai terendah adalah 5.

Range = Nilai tertinggi - Nilai terendah = 75 - 5 = 70

5. Kuartil:

Kuartil kedua (Q2) adalah median = 36.5.
Kuartil pertama (Q1) adalah median dari separuh pertama data = 25.
Kuartil ketiga (Q3) adalah median dari separuh kedua data = 50.

6. Standar Deviasi:

Pertama, hitung mean = 36.5.
Kemudian hitung selisih kuadrat dari mean untuk setiap nilai:

(5-36.5)² + (12-36.5)² + ... + (75-36.5)²

Rata-rata selisih kuadrat:

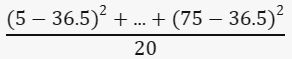contoh Foto: Edward R/detikSulsel

Standar deviasi adalah akar kuadrat dari rata-rata selisih kuadrat:

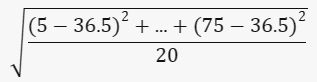contoh Foto: Edward R/detikSulsel

7. Variansi:

Variansi adalah kuadrat dari standar deviasi.

8. Koefisien Variasi:

Koefisien variasi dihitung dengan membagi standar deviasi dengan mean:

Koefisien Variasi = Standar Deviasi/Mean X 100%

Dengan menggunakan statistika deskriptif, pemerintah kota dapat memahami distribusi umur penduduk dan merencanakan layanan sesuai dengan kebutuhan berbagai kelompok umur. Misalnya, jika terdapat banyak penduduk usia lanjut, maka perlu ada peningkatan fasilitas kesehatan untuk kelompok umur tersebut.

6. Contoh Perhitungan Statistika Deskriptif dalam Dunia Pariwisata

Kasus: Sebuah kota wisata ingin menganalisis jumlah pengunjung bulanan ke sebuah objek wisata populer untuk mengevaluasi tren dan musim puncak kunjungan.

Data Jumlah Pengunjung (per bulan): 1200, 1400, 1300, 1500, 1600, 1700, 1800, 1900, 2000, 2100, 2200, 2300

1. Mean (Rata-rata):

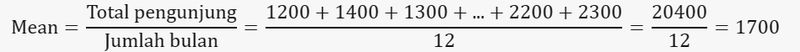contoh Foto: Edward R/detikSulsel

2. Median:

Data setelah diurutkan: 1200, 1300, 1400, 1500, 1600, 1700, 1700, 1800, 1900, 2000, 2100, 2200, 2300.

Median adalah nilai tengah, jadi median = 1700.

3. Modus:

Tidak ada nilai yang muncul lebih dari satu kali, sehingga tidak ada modus.

4. Rentang (Range):

Nilai tertinggi adalah 2300 dan nilai terendah adalah 1200.

Range = Nilai tertinggi - Nilai terendah = 2300 - 1200 = 1100

5. Kuartil:

Kuartil kedua (Q2) adalah median = 1700.
Kuartil pertama (Q1) adalah median dari separuh pertama data = 1400.
Kuartil ketiga (Q3) adalah median dari separuh kedua data = 2000.

6. Standar Deviasi:

Pertama, hitung mean = 1700.

Kemudian hitung selisih kuadrat dari mean untuk setiap nilai:

(1200-1700)² + (1300-1700)² + ... + (2300-1700)²

Rata-rata selisih kuadrat:

(1200-1700)² + ... + (2300-1700)² / 12

Standar deviasi adalah akar kuadrat dari rata-rata selisih kuadrat:

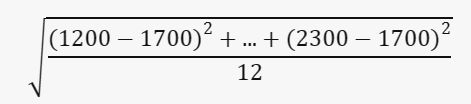contoh Foto: Edward R/detikSulsel

7. Variansi:

Variansi adalah kuadrat dari standar deviasi.

8. Koefisien Variasi:

Koefisien variasi dihitung dengan membagi standar deviasi dengan mean:

Koefisien Variasi = Standar Deviasi/Mean X 100%

Dengan menganalisis data ini, pihak pengelola objek wisata dapat mengetahui bulan-bulan dengan jumlah pengunjung tertinggi dan terendah, serta seberapa konsisten kunjungan dari bulan ke bulan. Informasi ini sangat berguna untuk merencanakan event, promosi, dan peningkatan fasilitas sesuai dengan kebutuhan pengunjung.

7. Contoh Statistika Deskriptif dalam Penjualan Toko Buku

Kasus: Sebuah toko buku ingin menganalisis frekuensi penjualan judul buku tertentu selama satu bulan.

Data Penjualan Buku (jumlah buku terjual per hari): 3, 7, 7, 2, 5, 7, 4, 3, 3, 6, 5, 7, 7, 3, 4, 2, 5, 7, 3, 7, 4, 3, 3, 5, 7, 2, 3, 7, 4, 5

1. Mean (Rata-rata):

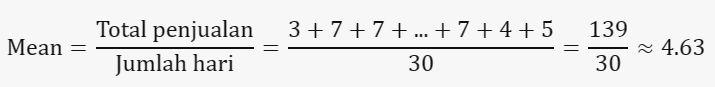contoh Foto: Edward R/detikSulsel

2. Median:

Data setelah diurutkan: 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5, 6, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7.

Median adalah nilai tengah, jadi median = 5.

3. Modus:

Nilai yang paling sering muncul adalah 7, sehingga modus = 7.

4. Rentang (Range):

Nilai tertinggi adalah 7 dan nilai terendah adalah 2.

Rang = Nilai tertinggi - Nilai terendah = 7 - 2 = 5

5. Kuartil:

Kuartil kedua (Q2) adalah median = 5.
Kuartil pertama (Q1) adalah median dari separuh pertama data = 3.
Kuartil ketiga (Q3) adalah median dari separuh kedua data = 7.

6. Standar Deviasi:

Pertama, hitung mean = 4.63.
Kemudian hitung selisih kuadrat dari mean untuk setiap nilai:

(3-4.63)² + (7-4.63)² + ... + (7-4.63)²

Rata-rata selisih kuadrat:

(3-4.63)² + ... + (7-4.63)² / 30

Standar deviasi adalah akar kuadrat dari rata-rata selisih kuadrat:

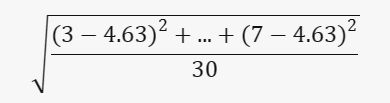contoh Foto: Edward R/detikSulsel

7. Variansi:

Variansi adalah kuadrat dari standar deviasi.

8. Koefisien Variasi:

Koefisien variasi dihitung dengan membagi standar deviasi dengan mean:

Koefisien Variasi = Standar Deviasi/Mean X 100%

Dengan perhitungan ini, toko buku dapat mengetahui judul buku mana yang paling laris (modus), seberapa besar variasi penjualan harian (standar deviasi dan variansi), dan seberapa konsisten penjualan tersebut relatif terhadap rata-rata (koefisien variasi). Informasi ini membantu dalam pengambilan keputusan terkait stok buku dan promosi penjualan.

Nah, itulah contoh perhitungan statistika deskriptif dalam berbagai bidang. Semoga bermanfaat ya, detikers!

Video: Pengumuman Angka Kemiskinan Ditunda, BPS Pastikan Tak Ada Pesanan

Video: Pengumuman Angka Kemiskinan Ditunda, BPS Pastikan Tak Ada Pesanan