Dalam ilmu statistik, rumus standar deviasi atau juga sering disebut simpangan baku kerap dijumpai. Seperti apa rumusnya? Berikut ini contoh soal standar deviasi lengkap dengan penjelasan mengenai fungsi dan jenisnya.
Dikutip dari buku Statistik Pendidikan karya Dr Rusydi Ananda dan Muhammad Fadhli, standar deviasi atau simpangan baku adalah salah satu cara yang bisa digunakan untuk mengukur variasi sekelompok data kuantitatif.
Semakin besar nilai standar deviasi, artinya semakin bervariasi angka-angka yang ada pada data kuantitatif terkait. Sebaliknya, standar deviasi yang rendah menunjukkan data lebih terkonsentrasi di sekitar rata-rata. Adapun lambang standar deviasi adalah SD.
SCROLL TO CONTINUE WITH CONTENT
Di bawah ini paparan lebih rinci seputar standar deviasi. Mulai dari fungsi, jenis, dan contoh soal rumus standar deviasi.
Fungsi Standar Deviasi
Dirangkum dari buku Statistik Deskriptif karya Tri Andjarwati dkk, standar deviasi digunakan sebagai salah satu ukuran penyebaran absolut. Sebabnya, ia bisa digunakan untuk membandingkan suatu rangkaian data dengan rangkaian data lainnya.
Lebih lanjut, ditilik dari detikEdu, standar deviasi juga bisa dipakai untuk mengetahui baik tidaknya data yang dimiliki seorang peneliti. Jika standar deviasinya kecil, maka data tersebut dibilang baik karena tidak terlalu tersebar ataupun menyimpang dari pusat data.
Jenis Rumus Standar Deviasi
Dihimpun dari modul Perkuliahan Sesi 7 Universitas Esa Unggul yang disusun oleh tim dosen, ada dua rumus standar deviasi data tunggal, yakni untuk populasi dan sampel. Ini rumusnya:
1. Rumus Standar Deviasi Populasi
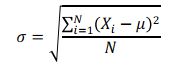 (Foto: Dok. Modul Perkuliahan Sesi 7 Universitas Esa Unggul oleh Tim Dosen) (Foto: Dok. Modul Perkuliahan Sesi 7 Universitas Esa Unggul oleh Tim Dosen) |
Penjelasan masing-masing lambangnya adalah sebagai berikut:
 (Foto: Dok. Modul Perkuliahan Sesi 7 Universitas Esa Unggul oleh Tim Dosen) (Foto: Dok. Modul Perkuliahan Sesi 7 Universitas Esa Unggul oleh Tim Dosen) |
2. Rumus Standar Deviasi Sampel
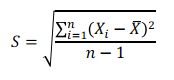 (Foto: Dok. Modul Perkuliahan Sesi 7 Universitas Esa Unggul oleh Tim Dosen) (Foto: Dok. Modul Perkuliahan Sesi 7 Universitas Esa Unggul oleh Tim Dosen) |
Keterangan:
 (Foto: Dok. Modul Perkuliahan Sesi 7 Universitas Esa Unggul oleh Tim Dosen) (Foto: Dok. Modul Perkuliahan Sesi 7 Universitas Esa Unggul oleh Tim Dosen) |
Contoh Soal Standar Deviasi
Masih diambil dari modul yang sama, ini contoh soal standar deviasi.
Soal:
Dari 40 orang siswa, diambil sampel 9 orang untuk diukur tinggi badannya. Diperoleh data: 165, 170, 169, 168, 156, 160, 175, 162, 169. Hitunglah standar deviasi sampelnya!
Pembahasan:
Pertama, hitung dahulu rata-rata sampelnya, yaitu:
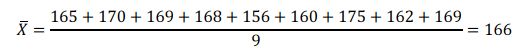 (Foto: Dok. Modul Perkuliahan Sesi 7 Universitas Esa Unggul oleh Tim Dosen) (Foto: Dok. Modul Perkuliahan Sesi 7 Universitas Esa Unggul oleh Tim Dosen) |
Setelahnya, hitung dengan rumus standar deviasi sampel. Untuk memudahkan hitungan, buat tabel terlebih dahulu.
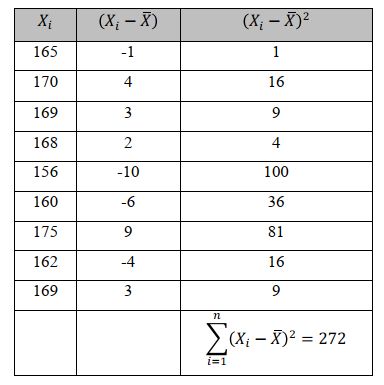 (Foto: Dok. Modul Perkuliahan Sesi 7 Universitas Esa Unggul oleh Tim Dosen) (Foto: Dok. Modul Perkuliahan Sesi 7 Universitas Esa Unggul oleh Tim Dosen) |
Terakhir, hitung nilai standar deviasinya.
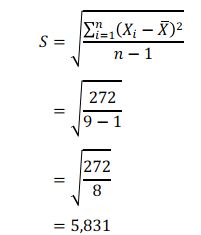 (Foto: Dok. Modul Perkuliahan Sesi 7 Universitas Esa Unggul oleh Tim Dosen) (Foto: Dok. Modul Perkuliahan Sesi 7 Universitas Esa Unggul oleh Tim Dosen) |
Jadi, nilai standar deviasinya adalah 5,831.
Demikian penjelasan mengenai standar deviasi. Dimulai dari pengertian, fungsi, sampai contoh soal dan pembahasannya. Semoga bermanfaat!
(sto/ams)
























































Komentar Terbanyak
Namanya Terseret di Sidang Ayahnya, Ini Kata Anak Eks Bupati Sleman Sri Purnomo
Jogja Diprediksi Ramai Wisatawan Saat Nataru, GKR Bendara Minta Akamsi Sabar
Istri dan Anak Eks Bupati Sleman Sri Purnomo Terseret Kasus Dana Hibah Rp 10 M