25 Contoh Soal TIU CPNS 2024 Plus dengan Pembahasannya, Yuk Kerjakan!

Yakni kemampuan verbal, kemampuan numerik dan kemampuan vigural. Agar terbiasa dan lancar dalam menghadapi SKD nanti, pelamar harus banyak berlatih soal-soal.

Seperti 25 contoh soal TIU CPNS berikut dikutip dari buku All New Tes CPNS 2024/2025 karya Tim Garuda Eduka dan Tim Mitrasiswa, Kamis (29/8/2024).

25 Contoh Soal TIU 2024

1. Sekutu : Kompetisi = Kolaborasi : ......

A. Persaingan
B. Teman
C. Pertandingan
D. Musuh
E. Lawan

Jawaban: A. Persaingan
Pembahasan: Sekutu memiliki makna yang berlawanan dengan Kompetisi. Sehingga makna yang berlawanan dengan Kolaborasi adalah Persaingan.

2. Pedas : Lombok = ...... : ......

A. Manis : Gula
B. Lapar : Makanan
C. Manis : Sirup
D. Kecap : Sakarin
E. Manisan : Teh

Jawaban: A. Manis : Gula
Pembahasan: Penas adalah rasa dari lombok sehingga manis adalah rasa dari gula.

3. Mengantuk : Tidur = .... : ....

A. Makanan : Kalori
B. Terbang : Berjalan
C. Polisi : Pencuri
D. Pelanggaran : Hukuman
E. Lapar : Makanan

Jawaban: A. Makanan : Kalori
Pembahasan: Ketika mengantuk menghasilkan tidur. Sehingga makanan menghasilkan kalori.

4. Kendaraan : Mobil = .... : ....

A. Binatang : Lawan
B. Kapal : Perahu
C. Gaji : Upah
D. Orang : Pemuda
E. Laut : Danau

Jawaban: D. Orang : Pemuda
Pembahasan: Salah satu jenis dari kendaraan adalah mobil. Sehingga hubungan yang tepat adalah orang dan pemuda karena salah satu jenis orang adalah pemuda.

5. Pernyataan "Jika Rina lulus ujian maka Rina akan menikah" sama dengan.....

A. Jika Rina lulus ujian maka Rina tidak menikah
B. Jika Rina tidak lulus ujian maka Rina akan menikah
C. Jika Rina tidak lulus ujian maka Rina tidak menikah
D. Jika Rina menikah maka Rina lulus ujian
E. Jika Rina tidak menikah maka Rina tidak lulus ujian

Jawaban: E. Jika Rina tidak menikah maka Rina tidak lulus ujian
Pembahasan: P = p -> q setara dengan -q -> -p
Sehingga jawabannya jika Rina tidak menikah, maka Rina tidak lulus ujian.

6. Jika bepergian ke Timbuktu maka harus datang ke Patena.
Jika datang ke Patena, maka harus melalui jembatan Torosi.

A. Sebagian yang datang ke Patena melalui jembatan Torosi
B. Sebagian yang pergi ke Timbuktu melalui jembatan Torosi
C. Semua yang melalui jembatan Torosi tentu bepergian ke Timbuktu
D. Semua yang bepergian ke Timbuktu harus melalui jembatan Torosi
E. Semua yang tidak bepergian ke Timbuktu tidak melalui jembatan Torosi

Jawaban: D. Semua yang bepergian ke Timbuktu harus melalui jembatan Torosi
Pembahasan: ini merupakan tipe soal silogisme dimana:

P1: p -> q
P2: q -> r
K : p -> r
Kesimpulannya semua yang bepergian ke Timbuktu harus melalui jembatan Torosi.

Untuk soal nomor 7-10 perhatikan ilustrasi berikut!

Asih, Bima, Cecep, Dedy dan Entin secara acak memiliki kesukaan terhadap olahraga futsal, voli, tenis, badminton, dan basket. Tiga dari mereka menyukai futsal. Masing-masing dari kelima anak itu menyukai dua olahraga yang berbeda. Tidak ada yang menyukai futsal juga menyukai tenis. Entin menyukai tenis. Hanya Asih dan Bima yang menyukai badminton dan apa yang disukai oleh Dedy pasti juga disukai oleh Cecep.

7. Bila Asih menyukai tenis maka pernyataan yang pasti benar adalah.....

A. Cecep menyukai tenis
B. Entin menyukai badminton
C. Bima menyukai futsal
D. Asih menyukai futsal
E. Bima menyukai basket

Jawaban: C. Bima menyukai futsal
Pembahasan: Jika Asih menyukai tenis maka didapatkan tabel kemungkinan olahraga kesukaan dari 5 orang anak tersebut yakni:

conntoh soal CPNS Foto: Buku Tes CPNS karya Tim Garuda Eduka dan Tim Mitrasiswa

Maka pernyataan yang pasti benar adalah "Bima menyukai futsal"

8. Bila Bima menyukai tenis maka pernyataan berikut yang salah adalah....

A. Cecep menyukai voli
B. Entin menyukai voli
C. Dedy menyukai basket
D. Asih menyukai voli
E. Dedy menyukai voli

Jawaban: D. Asih menyukai voli
Pembahasan: Jika Bima menyukai tenis maka didapatkan tabel kemungkinan olahraga kesukaan dari 5 orang anak tersebut yakni:

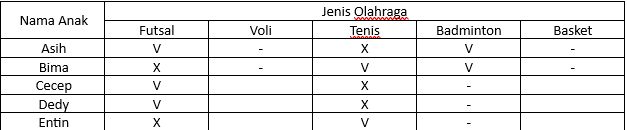conntoh soal CPNS Foto: Buku Tes CPNS karya Tim Garuda Eduka dan Tim Mitrasiswa

Maka pernyataan yang pasti salah adalah Asih menyukai voli.

9. Bila Entin menyukai basket maka pernyataan berikut yang salah adalah.....

A. Cecep menyukai tenis
B. Cecep menyukai voli
C. Bima menyukai basket
D. Asih menyukai futsal
E. Dedy menyukai voli

Jawaban: A. Cecep menyukai tenis
Pembahasan: Jika Entin menyukai basket maka didapatkan tabel kemungkinan olahraga kesukaan dari 5 orang anak tersebut yakni:

conntoh soal CPNS Foto: Buku Tes CPNS karya Tim Garuda Eduka dan Tim Mitrasiswa

Maka pernyataan yang pasti salah adalah Cecep menyukai tenis

10. Pernyatan berikut yang tidak mungkin terjadi adalah.....

A. Cecep menyukai voli
B. Entin menyukai voli
C. Bima menyukai basket
D. Asih menyukai futsal
E. Dedy menyukai tenis

Jawaban: E. Dedy menyukai tenis
Pembahasan: sesuai dengan syarat batas pada soal, Cecep dan Dedy memiliki kesukaan yang sama sehingga 2 dari 3 orang anak yang menyukai futsal pasti adalah keduanya. Jika menyukai futsal berarti tidak menyukai tenis. Jadi, pernyataan berikut yang tidak mungkin terjadi adalah "Dedy menyukai tenis"

Untuk soal nomor 11-14, perhatikan ilustrasi berikut!

Rahmat, Rina, Reni, Rendra, dan Raharja adalah siswa kelas VIII di SMP Ramandika. Mereka selalu belajar bersama dalam satu grup belajar. Hari ini adalah pembagian hasil ujian Kimia dan nilai mereka semua cukup memuaskan. Hasilnya nilai Rahmat lebih dari nilai Reni. Nilai Raharja kurang dari nilai Rendra. Tidak ada anak yang nilainya sama. Anak yang nilainya paling tinggi akan menjadi ketua grup.

11. Jika Rina berada pada peringkat ketiga di antara lima siswa tersebut maka....

A. Raharja bukan pada urutan pertama
B. Rahmat bukan pada urutan kedua
C. Rendra pada urutan pertama
D. Reni pada urutan keempat
E. Reni adalah yang terakhir

Jawaban: A. Raharja bukan pada urutan pertama
Pembahasan: syarat batas nilai dengan tidak ada nilai sama:
Rahmat > Reni
Rendra > Raharja
Tertinggi = ketua
Jika Rina berada pada peringat ketiga maka Raharja bukan pada urutan pertama karena nilainya selalu lebih rendah dari Rendra.

12. Jika yang menjadi ketua grup adalah Rahmat maka.....

A. Nilai Reni lebih dari nilai Rendra
B. Nilai Raharja kurang dari nilai Reni

C. Nilai Rina kurang dari nilai Rahmat
D. Nilai Rendra adalah yang tertinggi
E. Nilai Raharja adalah yang terendah

Jawaban: C. Nilai Rina kurang dari nilai Rahmat
Pembahasan: syarat batas nilai dengan tidak ada nilai sama:
Rahmat > Reni
Rendra > Raharja
Tertinggi = ketua
Sehingga jika Rahmat menjadi ketua grup berarti nilainya paling tinggi dan nilai Rina pasti kurang dari nilai Rahmat.

13. Jika nilai Reni lebih dari nilai Rendra maka ......

A. Rahmat adalah yang nilainya tertinggi
B. Rina nilainya paling bahwah
C. Nilai Rendra lebih dari nilai Rahmat
D. Nilai Rina lebih dari nilai Rendra
E. Nilai Reni lebih dari nilai Raharja

Jawaban: E. Nilai Reni lebih dari nilai Raharja
Pembahasan: syarat batas nilai dengan tidak ada nilai sama:
Rahmat > Reni
Rendra > Raharja
Tertinggi = ketua
Jika nilai Reni lebih dari nilai Rendra, maka nilai Reni lebih dari nilai Raharja.

14. Jika nilai Raharja lebih dari nilai Reni maka ....

A. Nilai Raharja lebih dari nilai Rahmat
B. Nilai Rina lebih dari nilai Reni
C. Nilai Reni adalah yang terendah
D. Nilai Reni kurang dari nilai Rendra
E. Nilai Rina adalah yang tertinggi

Jawaban: D. Nilai Reni kurang dari nilai Rendra
Pembahasan: Syarat batas nilai dengan tidak ada nilai sama:
Rahmat > Rani
Rendra > Raharja
Tertinggi = Ketua
Jika nilai Raharja lebih dari nilai Reni maka nilai Reni kurang dari Nilai Rendra

15. Jika rata-rata x, y, dan 30 adalah 10 maka rata-rata x dan y adalah .....

A. 10
B. 0
C. 5
D. 7,5
E. 8

Jawaban: B. 0
Pembahasan:
Maka rata-rata x dan y adalah:
10 = x + y + 30/3
30 = x + y + 30
x + y = 30 - 30
x + y = 0

Karena x + y bernilai nol maka rata-rata juga nol.

16. a + b = 30, hasil kali maksimum a dan b adalah .....

A. 175
B. 225
C. 275
D. 125
E. 100

Jawaban: B. 225
Pembahasan: untuk menentukan perkalian terbesar dapat diuji dengan memisalkan nilai a dan b, seperti:

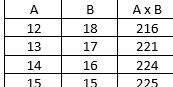conntoh soal CPNS Foto: Buku Tes CPNS karya Tim Garuda Eduka dan Tim Mitrasiswa

Jadi, hasil kali terbesar nilai a dan b adalah 225

17. 42, 38, 32, 49, 44, 32, ...., ...., 32, 63

A. 52, 50
B. 54, 56
C. 56, 50
D. 56, 52
E. 58, 58

Jawaban: C. 56, 50
Dalam deret ditemukan tiga pola beruntun dengan penjelasan:

pola (1)

Angka pertama yakni 42. Dengan ketentuan seling dua angka berarti angka selajutnya adalah 49. Selisih antara 42 dan 49 adalah 7. Sehingga setiap seling dua angka akan +7, seperti:

42 + 7 = 49
49 + 7 = 56

pola (2)

Angka pertama di pola dua adalah 38. Dengan ketentuan seling dua angka di dalam deret berarti angka selanjutnya adalah 44. Selisih antara 44 dan 38 adalah 6. Sehingga setiap seling dua angka akan +6, seperti:

38 + 6 = 44
44 + 6 = 50
dan selanjutnya

pola (3)

Angka pertama di pola ketiga adalah 32. Dengan ketentuan seling dua angka di dalam deret, berarti angka selanjutnya adalah 32. Selisih antara 32 dan 32 adalah 0. Sehingga setiap seling dua angka akan +0, seperti

32 + 0 = 32
dan seterusnya.

18. A, C, E, G, I, K, M, O, Q, S, ...., .....

A. V, W
B. U, W
C. S, W
D. U, X
E. V, X

Jawaban: B. U, W
Pembahasan: Pola yang ditemukan adalah huruf awal +2. Sehingga jawaban yang tepat adalah U dan W

19. 8, 8, 16, 24, 40, ...., .....

A. 64, 104
B. 72, 108
C. 76, 104
D. 80, 100
E. 82, 108

Jawaban: A. 64, 104
Pembahasan: Pola yang ditemukan adalah penambahan 2 angka sebelumnya sehingga:
8 + 0 = 8
8 + 8 = 16
16 + 8 = 24
24 + 16 = 40
40 + 24 = 64
64 + 40 = 104

20. A, K, C, N, E, Q, ....., ......, I

A. F, T
B. G, T
C. G, S
D. H, S
E. H, U

Jawaban: B. G, T
Bila dilihat deret ini memiliki pola seling antar huruf + 2 dan +3, sehingga:

pola 1 (+2)

2 huruf setelah A adalah C
2 huruf setelah C adalah E
sehingga 2 huruf setelah E adalah G

pola 2 (+3)

dimulai dari huruf K. Tiga huruf setelah K adalah N
Tiga huruf setelah N adalah Q
Sehingga tiga huruf setelah Q adalah T

21. Pak Yuda membeli 12 kg beras, 8 kg gula, dan 4 bungkus teh seharga Rp 104.000, sedangkan Pak Fahmi membeli 4 kg beras, 4 kg gula, dan 2 bungkus teh seharga Rp 44.000. Berapakah harga 1 kg beras?

A. Rp 3.500
B. Rp 3.750
C. Rp 4.200
D. Rp 4.000
E. Rp 4.250

Jawaban: D. Rp 4.000
Pembahasan:
Misal beras= x, gula = y, teh = Z
Diperoleh persamaan sebagai berikut:
12x + 8y + 4t = 104.000 (1)
4x + 4y + 2t = 44.000 (2)

Eliminasi kedua persamaan dan diperoleh:

12x + 8y + 4t = 104.000 (x1)
4x + 4y + 2t = 44.000 (x2)

12x + 8y + 4t = 104.000
8x + 8y + 4t = 88.000
-------------------------- (-)
4x = 16.000
x = 16.000/4 = 4000

Jadi, harga 1 kg beras adalah Rp 4.000

22. Berapakah biaya yang diperlukan untuk mengecat dinding dengan panjang 13 m dan tingginya 4 m jika per m^2 diperlukan biaya RP 4.500?

A. Rp 207.000
B. Rp 216.000
C. Rp 223.000
D. Rp 234.000
E. Rp 243.000

Jawaban: D. Rp 234.000
Pembahasan:
Biaya cat = luas x harga
Biaya cat = (13x4) x 4.500
Biaya cat = 52 x 4.540
Biaya cat = 234.000

23. Jika A luas lingkaran berjari-jari 5 cm dan B luas segi enam beraturan bersisi 5 cm maka.....

A. A < B
B. A > B
C. A = B
D. hubungan A dan B tidak dapat ditentukan
E. 3A = 7B

Jawaban: B. A > B
Pembahasan:
A = luas lingkaran berjari-jari 5 cm
B = luas segi enam beraturan bersisi 5 cm
Hubungan nilai A dan B diperoleh sebagai berikut:

A = πr^2
A = 22/7(5)^2
A = 78,57

Segi enam beraturan memiliki 6 segitiga kecil sama sisi dengan sisi 5, tinggi segitiga kecil yakni:

t = √5^2 - (5/2)^2
t - 4,33

Luas segi enam beraturan diperoleh:

B = 6 (5x4,33/2)
B = 64,95

Maka didapat nilai A > B

24. Seorang peternak memiliki anak ayam dan anak bebek sebanyak 400 ekor. 30% dari jumlah tersebut adalah anak bebek. Setelah peternak itu menjual anak ayamnya, persentase anak bebeknya 60%. Berapa ekor anak ayam yang dijual?

A. 200 ekor
B. 180 ekor
C. 160 ekor
D. 140 ekor
E. 120 ekor

Jawaban: A. 200 ekor
Pembahasan:
Jumlah anak bebek + anak ayam = 400 ekor

Jumlah anak bebek = 30%
maka jumlah anak ayam = 70%
Sehingga diperoleh:
Jumlah bebek = 30/100 x 400 = 120 ekor
Jumlah ayam = 70/100 x 400 = 280 ekor

Setelah anak ayam dijual, jumlah total anak ayam dan anak bebek = A
Jumlah anak bebek = 60% dari A
Maka diperoleh:
Jumlah bebek = 60% x A
120 ekor = 60/100 x A
A = 120 x 100/60
A = 200 ekor

Jumlah sisa anak ayam: 200-120 = 80 ekor
Jumlah ayam yang dijual = 280-80 = 200 ekor

Jadi, jumlah anak ayam yang dijual adalah 200 ekor.

25. Sebuah mobil bergerak dengan kecepatan tetap, untuk menempuh jarak sejauh 30 km menghabiskan bensin sebanyak 5 liter. Berapa liter bensin yang diperlukan jika jarak yang ditempuh sejauh 90 km?

A. 15 liter
B. 16 liter
C. 17 liter
D. 18 liter
E. 19 liter

Jawaban: A. 15 liter
Pembahasan:
jarak 30 km = bensin 5 liter
jarak 90 km = bensin ? liter

Oleh karena semakin jauh jarak semakin banyak volume bensi yang terpakai, maka:

30/90 = 5/x
3/9 = 5/x
x = 15 liter

Jadi, untuk menempuh jarak sejauh 90 km akan menghabiskan bensin sebanyak 15 liter.

Itulah 25 contoh soal TIU CPNS 2024. Selamat berlatih!

Video: BKN soal Ada yang Terlanjur Resign Padahal Pengangkatan CPNS Diundur

Video: BKN soal Ada yang Terlanjur Resign Padahal Pengangkatan CPNS Diundur