Contoh Soal Pengetahuan Kuantitatif SNBT 2023 Lengkap dengan Pembahasan

Try out SNBT detikEdu Lets Try It Out — Foto: Foto: Try out SNBT detikEdu 'Let's Try It Out' (Trisna Wulandari/detikcom)

Jakarta -

Pada Seleksi Nasional Berdasarkan Tes (SNBT) 2023, terdapat subtes pengetahuan kuantitatif yang terdiri atas 15 soal dengan durasi pengerjaan 20 menit.

Menurut laman Seleksi Nasional Penerimaan Mahasiswa Baru (SNPMB), soal pengetahuan kuantitatif tidak sama dengan penalaran kuantitatif.

Tes pengetahuan kuantitatif adalah tes kedalaman pengetahuan mengenai matematika yang didapat dari pembelajaran. Pengetahuan ini mewakili kemampuan memakai informasi kuantitatif dan memanipulasi simbol-simbol angka. Kemampuan itu meliputi pengetahuan tentang ukuran perhitungan matematika, pemecahan masalah matematika, dan pengetahuan umum matematika.

SCROLL TO CONTINUE WITH CONTENT

Maka, pengetahuan kuantitatif pada umumnya adalah sekumpulan pengetahuan matematika seseorang, termasuk kemampuan melakukan hitungan matematika.

Sementara, penalaran kuantitatif adalah kemampuan menalar secara induktif dan deduktif dalam pemecahan masalah berupa angka.

Nah, bagi detikers yang tahun ini akan mengikuti SNBT 2023, yuk berlatih mengerjakan soal-soal pengetahuan kuantitatif berikut ini!

Contoh Soal Pengetahuan Kuantitatif SNBT 2023

Menghimpun dari Simulasi SNBT SNPMB, ini dia contoh-contoh soal sekaligus pembahasannya:

1. Bilangan yang habis dibagi 3, tapi tidak habis dibagi 5 adalah...

A. 13689

B. 12345

C. 15223

D. 20579

E. 14670

Pembahasan:

Ciri bilangan yang habis dibagi tiga adalah jumlah angka pembentuknya kelipatan 3. Sementara, ciri bilangan yang habis dibagi 5 adalah angka satuannya 0 atau 5.

13689: habis dibagi 3, tetapi tidak habis dibagi 5 (benar).

12345: habis dibagi 3 dan habis dibagi 5 (salah).

15223: tidak habis dibagi 3 dan tidak habis dibagi 5 (salah).

20579: tidak habis dibagi 3 dan tidak habis dibagi 5 (salah).

14670: habis dibagi 3 dan habis dibagi 5 (salah).

Jawaban: A

2. Kurva y = ax² + 2x + 1 dengan a ≠ 0 memotong sumbu-x di dua titik berbeda. Pernyataan yang benar adalah ....

A. kurva terbuka ke atas

B. kurva memotong sumbu-y negatif

C. titik puncak kurva berada di kuadran I

D. kurva terbuka ke bawah

E. kurva memotong sumbu-y positif

Pembahasan:

Jika x=0. maka y=1 sehingga kurva memotong sumbu -y positif

Jawaban: E

3. Kurva y = ax² + 2x + 1 dengan a ≠ 0 memotong sumbu-x di dua titik berbeda.

Pernyataan yang benar adalah ....

A. a < 1

B. 3a > 1

C. 3a > 2

D. 6a < 1

E. a > 1

Pembahasan:

Apabila kurva y = ax² + 2x + 1 dengan a ≠ 0 memotong sumbu-x di dua titik berbeda, maka 2² - 4a(1) > 0, sehingga a < 1.

Jawaban: A.

4. Garis dengan persamaan mana saja yang memotong garis 2x + y = 4 dan x + 2y = 2 di dua titik berbeda?

1) y = -x + 5
2) y = x - 2
3) y = 3x -1
4) y = -2x + 7

A. (1) dan (3) SAJA yang benar.

B. (2) dan (4) SAJA yang benar.

C. (1), (2), dan (3) SAJA yang benar.

D. HANYA (4) yang benar.

E. SEMUA pilihan benar.

Pembahasan:

Gradien garis 1 tidak sama dengan gradien garis 2, sehingga garis ketiga memotong dua garis tersebut di dua titik berbeda apabila:

(a) gradiennya berbeda dengan kedua gradien garis yang lain, dan

(b) tidak melalui titik potong dua garis yang lain.

Jadi, garis dengan persamaan (1) atau persamaan (3) memotong dua garis lainnya di dua titik berbeda.

Jawaban: A.

5. Terdapat kumpulan data 3,5,7, a. Berapakah banyaknya dari empat pernyataan berikut yang bernilai benar berdasarkan informasi ini?

1) Rata-rata kumpulan data tersebut 6 bila a=9.

2) Median kumpulan data tersebut 5 bila a=7.

3) Jangkauan kumpulan data tersebut 4 bila a=6.

4) Modus kumpulan data tersebut 3 bila a=5

A. 4

B. 0

C. 3

D. 1

E. 2

Pembahasan:

- Rata-rata adalah 6
- Median adalah 6
- Jangkauan adalah 4
- Modus adalah 5

Sehingga, pernyataan yang benar ada 2, yaitu pernyataan (1) dan (3).

Jawaban: E

6. Tiga bola diambil dari sebuah kotak yang berisi 3 bola merah dan 2 bola putih. Misalnya B menyatakan kejadian terambilnya 2 bola merah dan 1 bola putih dan P(B) menyatakan peluang kejadian B.

Berdasarkan informasi tersebut, manakah hubungan antara kuantitas P dan Q berikut yang benar?

Soal nomor 6. Foto: SNPMB

A. Q > P

B. P = Q

C. P > Q

D. Tidak dapat ditentukan hubungan

Pembahasan:

Peluang terambilnya 2 bola merah dan 1 bola putih adalah:

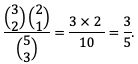soal nomor 6 Foto: SNPMB

Jawaban: C

7. Bilangan riil x memenuhi pertidaksamaan 2x+1<4.
Berdasarkan informasi yang diberikan, manakah hubungan antara kuantitas P dan Q berikut yang benar?

Soal nomor 7. Foto: SNPMB

A. Q > P

B. P = Q

C. P > Q

D. Tidak dapat ditentukan hubungan

Pembahasan:

2x + 1 < 4 → 2x < 3 → -2x > -3

Maka, -2x bisa lebih dari atau kurang dari atau sama dengan 2 sehingga tidak bisa ditentukan hubungan antara kualitas P dan Q.

Jawaban: D

8. Diketahui segitiga ABCD dengan ∠B = 30º.
Apakah segitiga ABC siku-siku?

Putuskan apakah pernyataan (1) dan (2) di bawah ini cukup untuk menjawab pertanyaan tersebut.

(1) ∠A - ∠C = 20°.

(2) ∠C < ∠A.

A. Pernyataan (1) dan pernyataan (2) tidak cukup untuk menjawab pertanyaan.

B. Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup.

C. Pernyataan (1) dan (2) cukup untuk menjawab pertanyaan, tetapi salah satu dari keduanya tidak cukup.

D. Pernyataan (1) atau pernyataan (2) SAJA sudah cukup untuk menjawab pertanyaan.

E. Pernyataan (2) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (1) SAJA tidak cukup.

Pembahasan:

∠A + ∠C = 180° - 30° = 150°

∠A - ∠C = 20°

Karena dua persamaan tersebut merupakan SPL yang konsisten, pertanyaan dapat dijawab. Pernyataan (1) cukup digunakan untuk menjawab pertanyaan

Karena ∠A + ∠C = 150°, pernyataan (2) tidak cukup untuk memutuskan apakah ∠A siku-siku.

Jawaban: B

9. Titik P dan Q berturut-turut terletak pada rusuk AB dan BC kubus ABCD.EFGH dengan PA:PB=1:2 dan BQ:QP=1:1.
Manakah dari tiga pernyataan berikut yang bernilai benar berdasarkan informasi di atas?

(1) Perbandingan volume limas PBQ.F dan volume kubus ABCD.EFGH =1:18 .

(2) Perbandingan luas ΔPBQ dengan luas persegi ABCD=1:6.

(3) PQ:AC = 1:√2 .

A. Pernyataan (1) dan (2) SAJA yang benar.

B. Pernyataan (2) dan (3) SAJA yang benar.

C. Pernyataan (3) SAJA yang benar.

D. Tidak ada pernyataan yang benar.

E. Semua pernyataan benar.

Pembahasan:

Volume limas PBQ.F : volume kubus ABCD.EFGH = ((1/2) x (2/3) x 1/2))/1 = 1: 18.

Luas ΔPBQ : luas persegi ABCD = ((1/2) x (2/3) x 1/2))/1

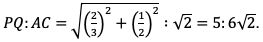Pembahasan soal nomor 8. Foto: SNPMB

Jadi, pilihan yang benar adalah pernyataan (1) dan (2).

Jawaban: A

10. Diketahui b = 2 x c dan b - d = 3.

Apakah d bilangan prima ?

Putuskan apakah pernyataan (1) dan (2) berikut cukup untuk menjawab pertanyaan tersebut.

(1) d = 2c - 3.

(2) b - 2c = 0.

A. Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup.

B. Pernyataan (1) atau pernyataan (2) SAJA sudah cukup untuk menjawab pertanyaan.

C. Pernyataan (2) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (1) SAJA tidak cukup.

D. Pernyataan (1) dan (2) cukup untuk menjawab pertanyaan, tetapi salah satu dari keduanya tidak cukup.

E. Pernyataan (1) dan pernyataan (2) tidak cukup untuk menjawab pertanyaan.

Pembahasan:

Pernyataan (1) didapat dari b = 2 x c dan b - d = 3.

Pernyataan (2) didapat dari b = 2 x c.

Karena sistem tersebut terdiri dari 2 persamaan yang memuat 3 variabel dan pernyataan (1) dan (2) didapat dari b = 2 x c dan b - d = 3, maka pernyataan (1) dan (2) tidak cukup untuk menjawab pertanyaan.

Jawaban: E

Itulah beberapa contoh soal SNBT yang bisa kalian kerjakan. Bagaimana detikers, apakah jawaban kalian betul semua?