Besaran Turunan dan Satuannya: Pengertian, Dimensi, Fungsi Beserta Contohnya

Pada saat mengukur sebuah benda tentu kita akan menemukan besaran-besaran yang menjadi ukuran benda tersebut. Besaran sendiri diklasifikasikan ke dalam dua kelompok yaitu besaran pokok dan besaran turunan.

Besaran pokok sendiri dipahami sebagai sebuah besaran yang tidak bergantung pada besaran lain. Sedangkan besaran turunan merupakan besaran yang diturunkan dari besaran pokok. Nah, kalian sudah mengetahui tentang besaran turunan belum nih?

Yuk, simak penjelasan terkait besaran turunan yang mengutip dari Kemdikbud dan buku Praktis Belajar Fisika karya Aip Saripudin, dkk.

Pengertian Besaran Turunan

Besaran turunan merupakan besaran yang satuan dan dimensinya diturunkan dari besaran pokok. Contohnya adalah volume sebuah balok merupakan panjang x lebar x tinggi. Panjang, lebar dan tinggi diketahui sebagai sebuah besaran pokok yang sama yaitu panjang. Sebabnya, dapat kita ketahui volume merupakan besaran yang diturunkan dari tiga besaran pokok.

Satuan Besaran Turunan

Besaran turunan ternyata tidak hanya memiliki satuan yang diturunkan dari besaran pokok. Ternyata besaran turunan juga memiliki nama satuannya sendiri. Tabel di bawah ini merupakan contoh besaran turunan beserta satuannya.

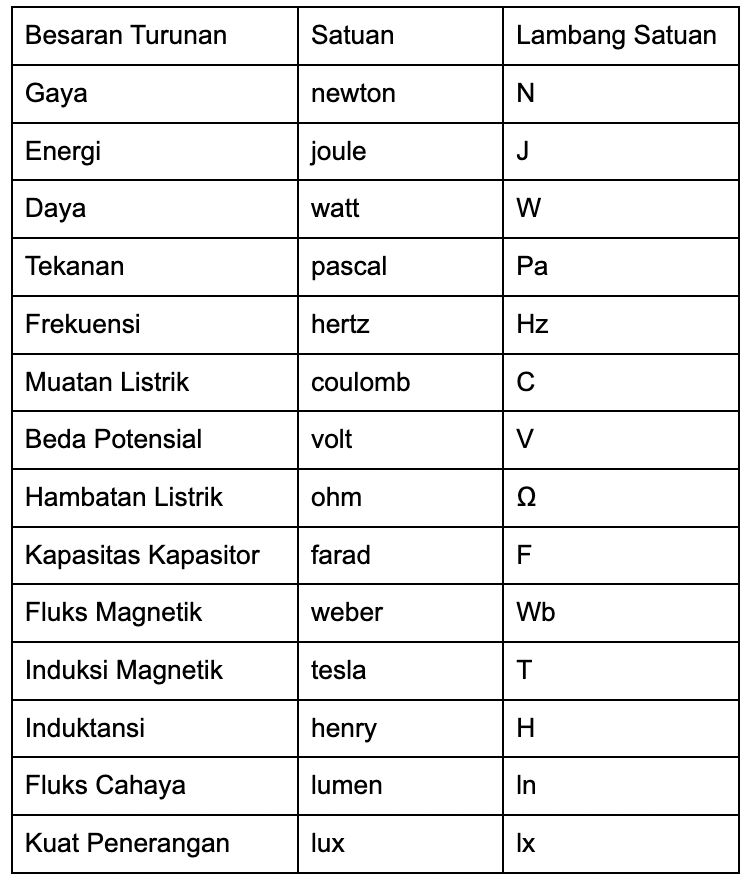Tabel satuan besaran turunan (Dok Kemendikbud) Foto: Tabel besaran turunan (Dok Kemendikbud)

Dimensi Besaran Turunan

Dimensi besaran dapat membantu kita untuk mengetahui bagaimana besaran tersebut diturunkan atau disusun dari besaran pokok. Pada sistem Satuan Internasional (SI), ada tujuh besaran pokok yang berdimensi, sedangkan dua besaran pokok tambahan tidak berdimensi.

Cara penulisan dimensi dari suatu besaran dinyatakan dengan lambang huruf tertentu dan diberi tanda kurung persegi. Seperti yang dapat kita lihat pada tabel berikut:

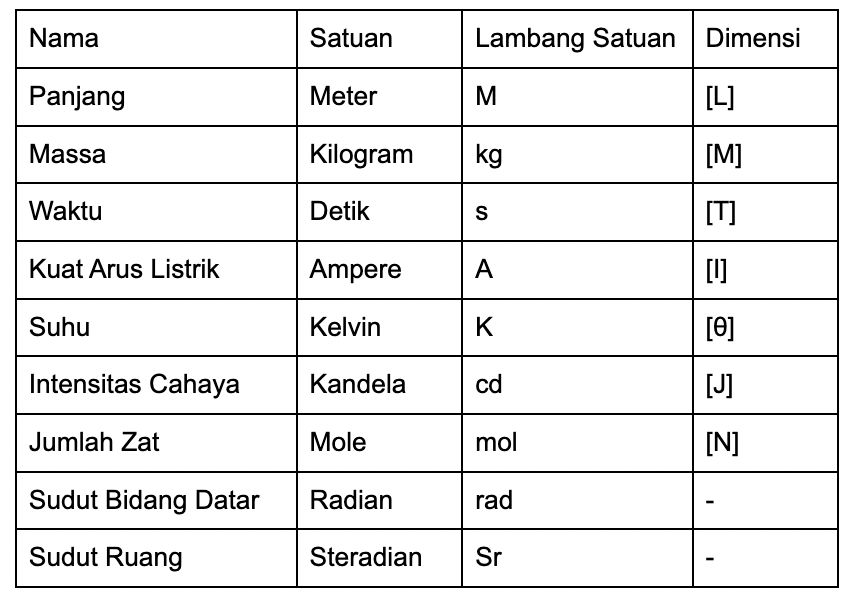Tabel besaran turunan (Dok Kemendikbud) Foto: Tabel besaran turunan (Dok Kemendikbud)

Fungsi Besaran Turunan

Besaran turunan yang merupakan turunan besaran pokok berfungsi untuk melengkapi besaran pokok. Besaran turunan sendiri dapat membantu kita untuk melakukan pengukuran yang lebih rumit dibandingkan besaran pokok.

Pada fisika besaran turunan digunakan untuk menghitung berbagai rumus seperti gaya, momentum, kecepatan, percepatan, volume, luas, hambatan listrik, muatan listrik, massa jenis, daya, usaha, dll.

Contoh Besaran Turunan

Berikut merupakan contoh besaran turunan yang diaplikasikan ke dalam dimensi:

Contoh:

Luas = panjang x panjang,

maka satuan luas = m x m = m²

Dimensi luas = L x L = L²

Laju = 𝐽𝑎𝑟𝑎𝑘/𝑊𝑎𝑘𝑡𝑢 (meter/second)

maka satuan laju = m/s = ms-¹

Dimensi laju = L/T = LT^-1

Massa jenis = 𝑚𝑎𝑠𝑠𝑎/𝑣𝑜𝑙𝑢𝑚𝑒 atau 𝜌 = 𝑚/𝑉,

maka satuan ρ = 𝑘𝑔/𝑚𝑥𝑚𝑥𝑚 = kgm^-3.

Dimensi ρ= 𝑀/𝐿×𝐿×𝐿 , jadi dimensi massa jenis adalah ML^-3.

Contoh Soal:

a. Untuk mengetahui apakah sebuah rumus benar atau salah

Rumus perpindahan s= v_o t + ½at², dengan s adalah perpindahan, v_o adalah kecepatan, a adalah percepatan dan t adalah waktu. Apakah rumus tersebut benar?

Penyelesaian:

Rumus tersebut mungkin benar jika dimensi ruas kanan sama dengan dimensi ruas kiri.

Ruas kiri: s dimensinya = L

Ruas kanan suku I: vo/t dimensinya = [LT^-1] [T] = L

Ruas kanan suku II: ½ at² dimensinya = [LT^-2] [T²] = L (keterangan: ½ tidak berdimensi)

Karena dimensi ruas kiri sama dengan dimensi ruas kanan, kesimpulannya rumus s= v_o t + ½at² benar secara dimensi.

b. Untuk menurunkan persamaan atau rumus

Jika sebuah batu diikat dengan tali lalu diputar horizontal, maka tangan kita harus terus menarik tali, tidak boleh kendor atau lepas. Artinya tangan kita mengerjakan gaya (F) pada batu melalui tali. Seberapa besar gaya atau tarikan tangan kita, dapat diduga tergantung pada massa batu (m), panjang tali (l) dan seberapa cepat berputar (v). Jadi bagaimana bentuk persamaan atau rumus yang menghubungkan F, m, l dan v?

Penyelesaian:

Dimensi gaya F = MLT^-2

massa m = M

panjang l = L

kecepatan v = LT^-1.

Dimensi ruas kanan = dimensi ruas kiri.

F = m^a l^b v^c

MLT^-2 = M^a L^b (LT^-1) ^c = M^a L^b+c T^-c

Perhatikan pangkat (eksponen)

M, L, T ruas kanan harus sama dengan ruas kiri.

Kita peroleh a = 1, b+c =1 dan c = 2.

Jadi a = 1, b = -1 dan c = 2.

Dengan demikian gaya tarik tangan kita dapat dirumuskan:
𝐹 = 𝒎𝒍 ^−𝟏𝒗 ^𝟐 = 𝒎𝒗 ^𝟐/l

Video Kemendiktisaintek: Peminat MIPA Itu Menurun Sekarang, Khususnya Fisika

Video Kemendiktisaintek: Peminat MIPA Itu Menurun Sekarang, Khususnya Fisika