.webp)
Geometri sering kita jumpai. Dalam kehidupan sehari-hari banyak kejadian yang memiliki pola tertentu sehingga membantu kita dalam beraktivitas. Contohnya dapat kita temukan dalam jumlah penduduk suatu wilayah.
Pertumbuhan penduduk pada suatu kota A, selalu meningkat 3 kali dari tahun sebelumnya. Hasil sensus penduduk tahun 2020 menunjukkan jumlah penduduk di kota tersebut adalah 900.000 jiwa. Pada kasus ini kita dapat menghitung Jumlah penduduk di suatu kota dari tahun ke tahun dapat diprediksi menggunakan barisan dan deret geometri.
Barisan merupakan barisan bilangan yang suku berikutnya didapat dari penambahan suku sebelumnya. Sedangkan deret adalah penjumlahan dari barisan. Barisan dan deret dibedakan menjadi aritmatika dan geometri. Artikel ini akan menjelaskan tentang deret geometri.
SCROLL TO CONTINUE WITH CONTENT
Rumus Deret Geometri
Agar lebih mudah memahami deret geometri, dapat dilihat contoh berikut:
Barisan geometri : 2, 6 , 18 , 54 , ... .
Deret geometri : 2 + 6 + 18 + 54 + ... .
Jumlah n suku pertama deret geometri ditulis dengan Sn
Jadi S1 = U1 = 2
S2 = U1 + U2 = 2 + 6 = 8
S3 = U1 + U2 + U3 = 2 + 6 + 18 = 26
S4 = U1 + U2 + U3 + U4 = 2 + 6 + 18 + 54 = 80
Sehingga rumus deret geometri dapat diformulasikan dengan
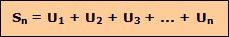 Rumus deret geometri yang bisa membantu siswa belajar matematika Foto: Sumber Belajar Kemdikbud |
Sedangkan rumus jumlah n suku pertama deret geometri ditemukan dengan:
Sn = U1 + U2 + U3 + ... + Un
Sn = a + (ar) + (ar2) + ... + arn-1
r x Sn = (ar) + (ar2) + .... + arn-1 + arn
-
Sn- r.Sn = a + 0 + 0 + + 0 + arn
(1 - r)Sn = a - arn
(1 - r)Sn = a (1 - rn)
 Rumus geometri Foto: Istimewa |
Contoh Soal Deret Geometri
Jumlah dari 400 + 200 + 100 + 50 + 25 + 12,5 = ...
Jawaban:
a = 400
r = 200 : 400
= 100 : 200
= ½
n = 6
Jadi jumlah dari 500 + 200 + 100 + 50 + 25 + 12,5 = 787,5
Itulah penjelasan deret geometri dan contoh soalnya, mudah kan. Sekarang coba detikers cari apa ada contoh deret geometri lain di sekitarmu?
(lus/lus)
