Pernahkah berpikir bagaimana cara menentukan titik tempat seperti di sebuah peta? Ternyata suatu benda atau objek yang ada di bumi dapat ditentukan posisinya dengan matematika, lho.
Salah satu metode yang dapat digunakan untuk menentukan posisi suatu benda adalah sistem koordinat. Lantas bagaimana cara menentukan sebuah titik koordinat?
Merangkum buku "Explore Matematika Jilid 2 untuk SMP/MTs Kelas VIII oleh Agus Supriyanto dan Miftahudin, berikut pengertian sistem koordinat, bidang kartesius serta cara mencari sebuah titik koordinat.
SCROLL TO CONTINUE WITH CONTENT
A. Sistem Koordinat
Sistem koordinat adalah suatu cara atau metode untuk menentukan letak suatu titik dalam grafik. Untuk mengetahuinya, simak gambar bidang koordinat di bawah ini.
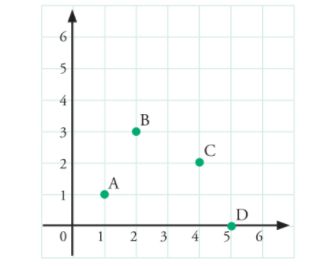 Gambar Bidang Koordinat dari buku Explore Matematika Jilid 2 untuk SMP/MTs Kelas VIII oleh Agus Supriyanto dan Miftahudin Foto: Screenshoot Gambar Bidang Koordinat dari buku Explore Matematika Jilid 2 untuk SMP/MTs Kelas VIII oleh Agus Supriyanto dan Miftahudin Foto: Screenshoot |
Bidang datar pada gambar disebut bidang koordinat yang dibentuk oleh garis tegak Y (sumbu Y) dan garis mendatar X (sumbu X).
Titik perpotongan antara garis Y dan X disebut pusat koordinat atau titik 0. Bidang koordinat tersebut dikenal dengan bidang koordinat Kartesius.
Bidang koordinat Kartesius digunakan untuk menentukan letak sebuah titik yang dinyatakan dalam pasangan bilangan.
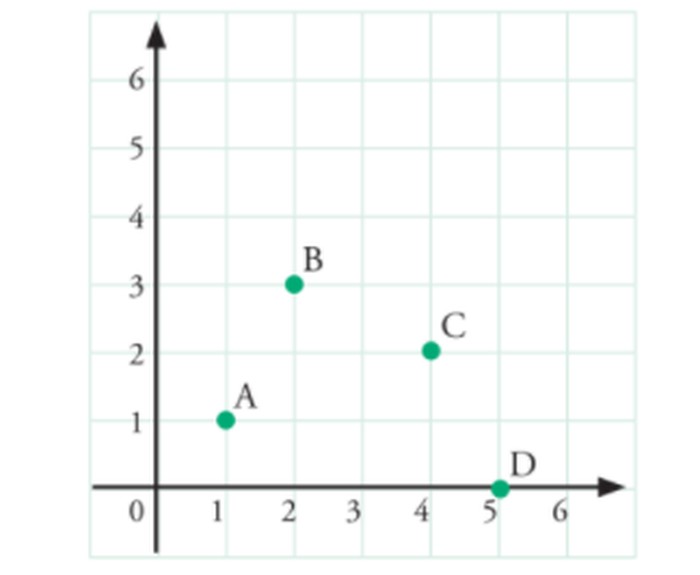
Perhatikan titik A, B, C, dan D yang ada pada bidang gambar di atas!
Letak titik-titik tersebut dapat ditentukan dengan bergerak dari titik 0. Dilanjutkan dengan bergerak ke arah kanan mendatar (sumbu X), kemudian bergerak ke atas (sumbu Y).
Letak titik pada bidang koordinat Cartesius ditulis dalam bentuk pasangan bilangan (x, y) dengan x disebut absis dan y disebut ordinat. Berdasarkan bidang koordinat pada Gambar 2.3 dapat ditentukan letak koordinat berikut.
- Titik A terletak pada koordinat (1. 1), ditulis A(1, 1).
- Titik B terletak pada koordinat (2, 3), ditulis B(2, 3).
- Titik C terletak pada koordinat (4, 2), ditulis (4. 2).
- Titik D terletak pada koordinat (5. 0), ditulis D(5, 0).
B. Bidang Koordinat Kartesius
Bidang koordinat Kartesius dapat dibagi menjadi 4 kuadran. Perhatikan gambar di bawah ini.
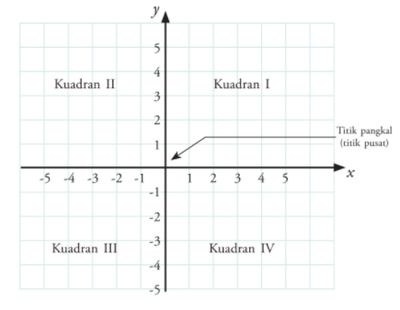 Kuadran pada Bidang Koordinat Kartesius dari buku Explore Matematika Jilid 2 untuk SMP/MTs Kelas VIII oleh Agus Supriyanto dan Miftahudin Foto: Screenshoot Kuadran pada Bidang Koordinat Kartesius dari buku Explore Matematika Jilid 2 untuk SMP/MTs Kelas VIII oleh Agus Supriyanto dan Miftahudin Foto: Screenshoot |
Pemisah antarkuadran disebut sumbu koordinat. Pada sumbu koordinat terdapat sumbu mendatar (horizontal) dan sumbu tegak (vertikal). Perpotongan kedua sumbu koordinat disebut titik pangkal (titik pusat).
Setiap sumbu koordinat terbagi menjadi ukuran satuan yang selanjutnya disebut koordinat. Koordinat di sebelah kanan titik pangkal memiliki nilai positif, sumbu koordinatnya disebut sumbu X positif.
Koordinat di sebelah kiri titik pangkal memiliki nilai negatif, sumbu koordinatnya disebut sumbu X negatif. Koordinat di atas titik pangkal memiliki nilai positif, sumbu koordinatnya disebut sumbu Y positif.
Sementara itu, koordinat di bawah titik pangkal memiliki nilai negatif, sumbu koordinatnya disebut sumbu Y negatif.
C. Cara Mencari Titik Koordinat
Diketahui koordinat titik P(-3, 4), Q(2, 4), R(2, -2), dan S(-3, -2).
a. Gambarkan titik-titik tersebut ke dalam bidang koordinat!
b. Jika keempat titik dihubungkan dengan ruas garis, bangun apa yang terbentuk?
Penyelesaian:
a. Gambar titik-titik pada bidang koordinat adalah sebagai berikut.
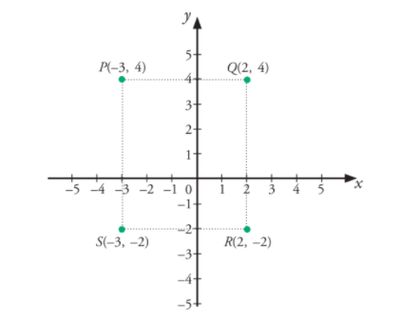 Jawaban gambar titik pada bidang koordinat Foto: Screenshoot Jawaban gambar titik pada bidang koordinat Foto: Screenshoot |
b. Bangun PQRS merupakan bangun segi empat. Oleh karena jarak titik P dengan titik Q tidak sama dengan jarak titik Q dengan titik R maka PQRS merupakan bangun persegi panjang.'
Nah itulah penjelasan mengenai titik koordinat matematika beserta jenis bidang kartesius dan contohnya. Semoga membantu ya detikers!
(faz/lus)