.webp)
Dalam matematika, kita mengenal yang namanya integral. Materi tentang integral diberikan saat duduk di bangku SMA. Mungkin kita bertanya-tanya mengapa integral harus dipelajari.
Ternyata penghitungan integral memiliki banyak manfaat dalam berbagai lini kehidupan. Dilansir dari dewey.petra.ac.id, sejarah integral diawali dari sejumlah ilmuwan. Antara lain Archimedes, seorang fisikawan dan matematika dari Yunani yang menemukan ide penjumlahan untuk menentukan luas daerah tertutup dan volume benda putar.
Kemudian Isaac Newton, fisikawan dan matematikawan dari Inggris, serta Gottfried Wilhelm Leibniz, ilmuwan dari Jerman yang mampu mengungkapkan hubungan antara antidiferensial dengan integral tertentu, yang sering dikenal sebagai Teorema Dasar Integral Kalkulus. Leibniz juga mengenalkan penggunaan lambang atau notasi matematika, seperti dx dy untuk turunan dan tanda ∫ untuk integral.
SCROLL TO CONTINUE WITH CONTENT
Ada juga Georg Friedrich Benhard Riemann, seorang matematikawan dari Jerman. Dia memberikan definisi mutakhir tentang integral tertentu. Atas temuannya inilah, integral sering juga disebut sebagai Integral Rieman.
Nah, di sini akan kita ulas apa itu integral dan apa saja jenis beserta rumusnya. Tak lupa sejumlah penerapan integral di segala bidang beserta contoh soalnya.
Pengertian Integral
Dilansir dari Modul Integral yang disusun Erfan Yudianto dalam repository.unej.ac.id, integral masih berhubungan dengan bab lain dalam matematika, yaitu diferensial.
Integral merupakan invers atau kebalikan dari diferensial. Dalam arti lain, integral adalah antiturunan dari proses hitung diferensial. Jika dalam diferensial kita terlebih dahulu mengetahui pernyataan kemudian mencari turunan, maka dalam integral kita mengetahui turunan terlebih dahulu untuk mencari pernyataan.
Rumus Integral
Ada dua jenis integral yang harus detikers ketahui. Yang pertama adalah integral tentu dan kedua adalah integral tak tentu. Keduanya akan kita bahas lebih lanjut di bawah.
Sebelum mengetahui rumusnya, pahami contoh konsep berikut ini terlebih dahulu. Fungsi ini memiliki bentuk umum f(x) = 2x3 . Setiap fungsi tersebut memiliki turunan f'(x) = 6x2. Menentukan fungsi f(x) dari f'(x) berarti menentukan antiturunan dari f'(x).
Jika f(x) adalah fungsi umum yang bersifat f'(x) = f(x), maka f(x) adalah antiturunan atau integral dari F'(x) = f(x).
Rumus Integral Tentu
Maksud dari integral tentu adalah sebagai berikut. Jika y = f(x) kontinu pada interval a ≤ x ≤ b yang berarti a sebagai batas bawah dan b sebagai batas atas, maka:
 rumus integral. Foto: unej.ac.id |
Misal f(x) dan g(x) merupakan fungsi-fungsi kontinu dari interval tertutup [a,b], maka integral tentu memiliki sifat umum seperti di bawah ini.
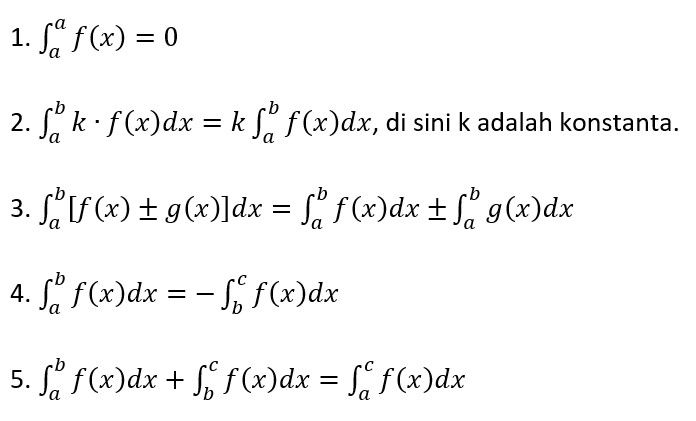 rumus integral. Foto: unej.ac.id |
Agar lebih jelas, berikut contoh soal terkait integral tentu.
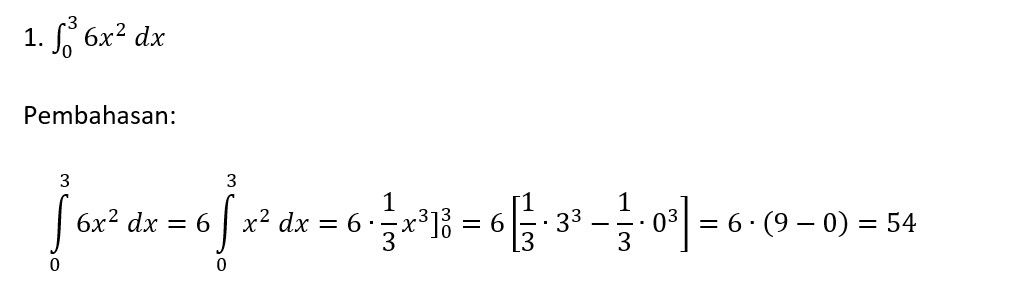 rumus integral. Foto: unej.ac.id |
 rumus integral. Foto: unej.ac.id |
Rumus Integral Tidak Tentu
Integral tak tentu maksudnya integral yang tidak memiliki batas. Berbeda dengan integral tertentu yang sudah kita bahas sebelumnya yang memiliki batas-batas.
Pengintegralan fungsi f(x) yang ditulis sebagai ∫ f(x)dx disebut integral tak tentu dari f(x). Kemudian apabila F(x) adalah antiturunan dari f(x), maka ∫ f(x)dx = F(x) + c, dengan c adalah konstanta .
Rumusnya ialah sebagai berikut:
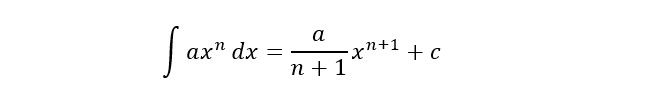 rumus integral. Foto: unej.ac.id |
Berikut contoh soal integral tak tentu.
Diketahui f'(x) = 6x2 - 10x + 3, dan f(-1) = 2, tentukan f(x)!
Pembahasan:
 rumus integral. Foto: unej.ac.id |
Penerapan Integral pada Kehidupan Sehari-hari
Integral memiliki manfaat yang besar dalam kehidupan sehari-hari. Dikutip dari artikel yang diunggah Haidir Agus dan DeArtha di Scribd, integral bisa diaplikasikan untuk berbagai hal di luar matematika, seperti fisika, biologi, teknik, teknologi dan ekonomi:
- Mengukur luas suatu bidang
- Menghitung volume benda putar
- Menentukan panjang panjang busur.
- Dapat digunakan untuk membuat desain mesin pesawat terbang.
- Di bidang ekonomi antara lain digunakan untuk mengetahui fungsi produksi, konsep elastisitas, angka pengganda, untuk mencari biaya marjinal.
- Dalam pembangunan gedung pencakar langit juga diperlukan integral agar bagian atas gedung tidak roboh diterpa angin kencang.
Teknik Integral
Salah satu teknik pengintegralan adalah teknik substitusi. Dalam Modul Integral yang disusun Erfan Yudianto dalam repository.unej.ac.id, disebutkan bahwa tak semua integral bisa dikerjakan dengan rumus di atas.
Dengan teknik substitusi, maka metode yang kompleks diubah dengan cara sederhana. Bentuk umum dari integral dengan teknik substitusi adalah sebagai berikut.
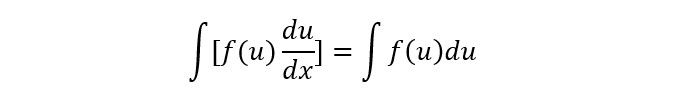 rumus integral. Foto: unej.ac.id |
Nah demikian tadi penjelasan mengenai integral beserta rumusnya dan penerapannya dalam bidang lain. Semoga bermanfaat ya.
(bai/row)
