Rumus Standar Deviasi: Pengertian, Fungsi, Jenis, dan Contoh

Dalam dunia statistik, memahami nilai variabilitas sangat penting untuk mengetahui tingkat akurasi rata-rata. Menurut Hariyadi (2009) dalam buku Statistik Pendidikan oleh Syafril, ada beberapa macam bentuk nilai variabilitas, yaitu jangkauan (range), mean deviasi, variansi, koefisien variansi, simpangan kuartil, dan standar deviasi (simpangan baku).

Standar deviasi (simpangan baku) merupakan salah satu alat statistik yang paling banyak digunakan. Maka dari itu, orang yang bekerja dalam bidang statistik harus memahami standar deviasi dengan baik.

Lalu, bagaimana cara menghitung standar deviasi? Ketahui lebih dalam tentang pengertian, fungsi dan rumus standar deviasi di artikel ini!

Pengertian Rumus Standar Deviasi

Standar deviasi atau simpangan baku adalah persebaran data pada suatu sampel untuk melihat seberapa jauh atau seberapa dekat nilai data dengan rata-ratanya. Standar deviasi pertama kali ditemukan oleh Karl Pearson pada tahun 1894 dan tercatat dalam bukunya berjudul On the Dissection of Asymmetrical Frequency Curves.

Dengan kata lain, standar deviasi adalah nilai akar kuadrat dari varians dan menunjukkan standar penyimpangan data terhadap nilai rata-ratanya. Jika nilai standar deviasi semakin kecil, artinya semakin mendekati rata-rata. Namun jika nilai standar deviasi semakin besar, artinya semakin lebar variasi datanya.

Fungsi Rumus Standar Deviasi

Standar deviasi digunakan untuk melihat jauh dekatnya sebaran data tersebut dari rata-rata atau mean. Salah satu fungsi rumus standar deviasi adalah memberikan gambaran tentang persebaran data terhadap rata-rata.

Dikutip dari buku Statistik Pendidikan oleh Syafril, standar deviasi adalah pengukuran variabilitas yang paling memenuhi persyaratan karena tidak membuang nilai yang ekstrem, menghitung penyimpangan nilai dari rata-rata dan memperhitungkan penyimpangan nilai negatif dan positif.

Mencari data yang tepat untuk suatu populasi sangat sulit dilakukan, sehingga perlu menggunakan sampel data yang dapat mewakili seluruh populasi untuk mempermudah penelitian.

Contohnya, jika Anda ingin mengetahui berat badan remaja perempuan berusia 15-17 tahun di sekolah. Hal pertama yang harus Anda lakukan adalah mendata berat badan beberapa orang, kemudian menghitung rata-rata dan standar deviasinya. Hasil perhitungannya akan menunjukan nilai yang mewakili seluruh populasi.

Jenis Rumus Standar Deviasi

Rumus standar deviasi dapat dihitung secara manual atau dengan Excel. Dikutip dalam buku berjudul Pengantar Statistika yang ditulis Romansyah Sahabuddin, rumus standar deviasi data tunggal dan kelompok antara lain:

1. Rumus Standar Deviasi Data Tunggal

Jenis data tunggal adalah data sederhana yang belum dikelompokkan ke dalam kelas interval. Rumus standar deviasi data tunggal adalah sebagai berikut:

Foto: Delweys Octoria/detikcom

2. Rumus Standar Deviasi Data Kelompok

Jenis data kelompok adalah data yang biasa ditampilkan dalam tabel frekuensi yang sudah dikelompokan dalam kelas interval. Rumus standar deviasi data kelompok adalah sebagai berikut:

Foto: Delweys Octoria/detikcom

Contoh Soal dan Pembahasan Rumus Standar Deviasi

Supaya lebih mengerti tentang standar deviasi, sekarang saatnya mencoba kerjakan soal tentang standar deviasi. Dikutip makalah berjudul 'Varian dan Standar Deviasi yang ditulis oleh Clara Dewi Larasati dan kawan-kawan, inilah contoh-contoh soal yang bisa Anda coba kerjakan. Ada pembahasannya juga, lho!

1. Contoh Soal Standar Deviasi Data Tunggal

Diketahui kumpulan data sebagai berikut 6, 7, 8, 8, 9, 10. Tentukan standar deviasi dari data tersebut!

Penyelesaian:

• Langkah pertama, hitung rata-rata (mean) dari data tersebut terlebih dahulu. Caranya dengan menjumlahkan data, kemudian dibagi dengan banyak data.

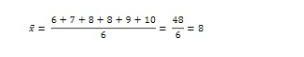Foto: Delweys Octoria/detikcom

• Setelah mendapat rata-ratanya yaitu 8, hitung varian populasinya. Varian merupakan ukuran variasi yang menunjukan penyebaran data dari rata-rata.

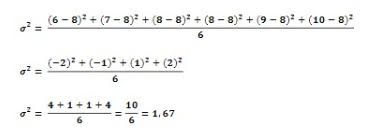Foto: Delweys Octoria/detikcom

• Setelah varian populasi ditemukan, barulah kita bisa menghitung standar deviasinya.

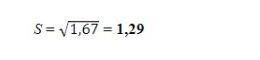Foto: Delweys Octoria/detikcom

• Dari soal tersebut, telah diketahui standar deviasinya yaitu sebesar 1,29.

2. Contoh Soal Standar Deviasi Data Kelompok

Diketahui data di bawah adalah data berat badan siswa SMA Angkasa kelas 12. Hitunglah standar deviasi dari tabel berikut!

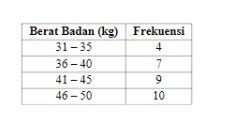Foto: Delweys Octoria/detikcom

Penyelesaian:

• Pertama, kita perlu menghitung nilai tengah dari data berat badan. Misalnya, cara menghitung nilai tengah data pertama adalah 31,32,33,34,35. Data tengahnya adalah 33.

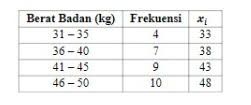Foto: Delweys Octoria/detikcom

• Setelah mendapatkan nilai tengahnya, kita kalikan nilai frekuensi dengan nilai tengah, kemudian buat juga tabel kuadratnya.

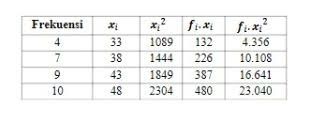Foto: Delweys Octoria/detikcom

• Jika sudah tersusun seperti itu, kita cari variannya.

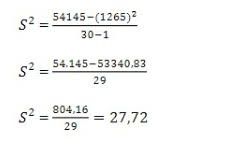Foto: Delweys Octoria/detikcom

• Setelah menemukan varian, barulah kita bisa menghitung standar deviasinya.

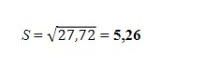Foto: Delweys Octoria/detikcom

Dari soal tersebut, telah diketahui standar deviasinya yaitu sebesar 5,26.

Nah, sekarang detikers sudah mengetahui rumus standar deviasi dan contoh-contoh soalnya. Menghitung standar deviasi tidak terlalu sulit, bukan? Anda bisa coba-coba soal lainnya sendiri untuk latihan. Semoga informasi ini bermanfaat, ya!

Pesona Wisata Sumenep: Pantai, Sejarah, dan Tradisi

Pesona Wisata Sumenep: Pantai, Sejarah, dan Tradisi