.webp)
Matriks adalah kelompok elemen berupa angka, simbol, huruf, dan sebagainya yang disusun dalam bentuk baris atau susunan horizontal dan kolom atau susunan vertikal. Kelompok tersebut harus membentuk persegi atau persegi panjang. Jika di luar bentuk tersebut, maka tidak bisa dikatakan sebagai matriks. Matriks dapat ditambah-kurangkan atau dikalikan. Pembeda matriks dengan kelompok bilangan lain adalah adanya tanda kurung biasa "( )" atau kurung siku "[ ]" sebagai pembingkai kelompok elemen matriks tersebut.
Menurut Zaini, SPd, MPd, dalam 'Determinan Matriks Persegi dan Non Persegi', penamaan matriks biasanya menggunakan huruf besar. Misalnya A atau B. Jumlah baris dan kolomnya menyesuaikan jumlah elemen yang tersedia.
Baris dan kolom dibedakan dengan huruf untuk memudahkan identifikasi bilangan yang ada dalam matriks tersebut. Misalnya menggunakan i untuk baris dan j untuk kolom, sehingga matriks tersebut dinotasikan i x j. Bisa juga menggunakan huruf m untuk baris dan n untuk kolom, sehingga matriks dikatakan berdimensi m x n.
Jumlah entri terkecil dalam suatu matriks adalah satu, sementara jumlah terbesarnya tidak dibatasi. Jumlah ini menentukan ordo atau ukuran dari suatu matriks. Misalnya jika ada 2 baris dan 3 kolom elemen, maka ordo matriks tersebut adalah 2 x 3 = 6 ordo.
SCROLL TO CONTINUE WITH CONTENT
Jenis-jenis Matriks
Berangkat dari jumlah ordo ini, ada beberapa jenis matriks yang dikenal. Antara lain:
- Matriks baris
- Matriks kolom
- Matriks persegi
- Matriks nol
- Matriks segitiga
- Matriks diagonal
- Matriks identitas atau satuan
- Matriks datar
- Matriks tegak
- Matriks skalar
- Penjumlahan dan Pengurangan Matrix
Matriks dapat dijumlahkan antara satu kelompok bilangan dengan kelompok bilangan lainnya yang sama-sama dikumpulkan dalam tanda kurung biasa maupun kurung siku. Mengutip Cuemath, penjumlahan matriks hanya bisa dilakukan apabila dua matriks atau lebih itu memiliki ukuran atau dimensi yang sama. Dalam artian, jumlah data atau bilangan dalam dua atau lebih matriks itu sama banyak. Begitu juga dengan pengurangan, hanya dapat dilakukan apabila kedua atau lebih matriks memiliki jumlah baris dan kolom yang sama.
Berdasarkan Cuemath, ada dua metode penjumlahan matriks yang dapat digunakan. Yang pertama adalah metode sederhana. Dengan metode ini, elemen-elemen dalam dua matriks atau lebih dijumlahkan sesuai dengan posisi baris dan kolom yang sama. Metode yang kedua adalah penambahan matriks secara langsung, yakni dilakukan dengan menghitung langsung dari jumlah matriks.
Metode pertama lebih mudah namun juga membutuhkan waktu lebih lama untuk menjumlahkan antara elemen dalam satu matriks dengan matriks lainnya. Anggaplah matriks pertama berdenotasi A = [aij] dan matriks kedua berdenotasi B = [bij], maka penjumlahan ini menggunakan rumus A + B = [aij] + [bij].
Sementara itu, metode kedua atau penjumlahan langsung lebih jarang digunakan dibandingkan metode sederhana. Penjumlahan ini menggunakan simbol tanda tambah dilingkari. Misalkan ada dua matriks, masing-masing berdenotasi X dan Y. X memiliki elemen m x n sementara Y memiliki elemen p x q. Maka jumlah X + Y = (m + p) x (n x q).
Sifat-sifat Operasi Bilangan Matriks
Untuk mengerjakan soal penjumlahan matriks, perlu diperhatikan sifat-sifat operasi bilangan khususnya penjumlahan pada matriks. Berikut sifat-sifat penjumlahan matriks selengkapnya seperti disusun oleh Musriah dalam 'Bahan Ajar Operasi Penjumlahan dan Pengurangan Matriks'.
- Bersifat komutatif. A + B = B + A
- Bersifat asosiatif. (A + B) + C = A + (B + C)
- Matriks O (nol) bersifat A + O = O + A = A
- Semua matriks positif yang ditambahkan dengan matriks negatif maka hasilnya matriks nol.
Contoh Soal Penjumlahan dan Pengurangan Matriks
Berikut contoh soal yang dapat teman-teman kerjakan dalam penjumlahan matriks.
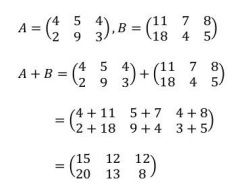 Contoh soal matriks. Foto: Musriah/SIMPPKB |
Pada contoh di atas, teman-teman menjumlahkan angka-angka pada matriks A dengan angka-angka pada matriks B yang posisinya sesuai. Misalnya 4 + 11 = 15. Maka 15 merupakan hasil penjumlahan dari baris pertama kolom pertama matriks A dan matriks B. Begitu seterusnya.
Metode yang sama juga dapat diterapkan untuk pengurangan matriks. Namun, perlu dicatat bahwa pengurangan matriks bersifat antikomutatif. Artinya jika A dikurangi B tidak sama dengan B dikurangi A. Berikut contoh soal pengurangan.
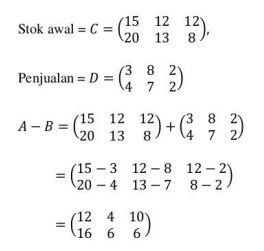 Contoh soal matriks. Foto: Musriah/SIMPPKB |
Pada contoh di atas, angka-angka pada matriks A dikurangkan dengan angka yang posisinya sesuai dengan matriks B.
Penjumlahan matriks ini dapat diterapkan untuk menghitung data mentah yang berbentuk baris dan kolom. Misalnya, seperti yang dicontohkan Musriah, terdapat data jumlah pembaca buku di perpustakaan berdasarkan usia pada baris dan jenis buku bacaan pada kolom. Angka-angka dalam tabel tersebut dapat diubah menjadi matriks apabila ada tabel pembanding lain yang perlu ditambahkan dengan tabel pertama.
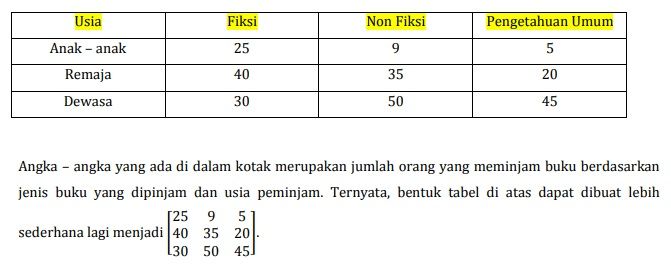 Contoh soal matriks. Foto: Musriah/SIMPPKB |
(des/fds)
