.webp)
Saat duduk di bangku Sekolah Menengah Atas (SMA) detikers pasti akan menemui pembelajaran persamaan kuadrat dalam matematika. Seperti apa contoh soal persamaan kuadrat?
Persamaan kuadrat merupakan persamaan dalam matematika yang memiliki variabel paling tinggi berderajat dua. Persamaan kuadrat juga memiliki jenis-jenis yang dibedakan dari akar-akarnya.
Dikutip dari buku 'Bahas Total Kumpulan Soal Super Lengkap Matematika SMA; oleh Supadi, berikut ini penjelasan mengenai persamaan kuadrat, lengkap dengan contoh soal persamaan kuadrat dan penyelesaiannya.
SCROLL TO CONTINUE WITH CONTENT
Bentuk Umum Persamaan Kuadrat
Persamaan kuadrat adalah persamaan yang variabel tertingginya berderajat dua. Bentuk umum persamaan kuadrat adalah:
ax² + bx + c = 0, dengan a, b, c, € R dan a ≠ 0
Keterangan:
- x adalah variabel
- a adalah koefisien dari x²
- b adalah koefisien dan x
- c adalah konstanta
Cara Menyelesaikan Persamaan Kuadrat
Untuk menyelesaikan sebuah contoh soal persamaan kuadrat, detikers harus memahami tiga cara menyelesaikan persamaan kuadrat: ax + bx+c= 0, yaitu:
1. memfaktorkan
2. melengkapkan kuadrat, dan
3. menggunakan rumus kuadrat (rumus abc), yaitu:
 Contoh Soal Persamaan Kuadrat dan Jawaban Materinya Foto: Screenshoot |
dengan:
D = b² - 4ac (D = diskriminan)
Jenis Akar-Akar Persamaan Kuadrat
Sebelum menyelesaikan contoh persamaan kuadrat, diperlukan untuk mengetahui persamaan kuadrat ax² + bx + c = 0, dengan akar-akar x1 dan x2 yang sangat bergantung pada nilai diskriminan (D).
- D ≥ 0 → persamaan kuadrat mempunyai dua akar nyata (real)
- D > 0 → persamaan kuadrat mempunyai dua buah akar nyata dan berbeda
- D = 0 → persamaan kuadrat mempunyai dua buah akar nyata yang sama (kembar)
- D < 0 → persamaan kuadrat tidak mempunyai akar nyata (akar imajiner)
Contoh Soal Persamaan Kuadrat
1) Persamaan kuadrat x² + (2m-1)x - 2m = 0, mempunyai akar-akar nyata dan berlainan. Batas-batas nilai m yang memenuhi adalah...
a. m < - 1⁄2
Persamaan kuadrat ax² + bx + c = 0 → akar-akar nyata dan berlainan jika D > 0. x² + (2m - 1)x - 2m = 0 → a = 1; b = 2m - 1, dan c = -2m. Memiliki akar-akar nyata dan berlainan (berbeda), maka berlaku (2m -1)² 4 . (1) . (-2m) > 0 = 2
b. - 1⁄2
c. m < - 1⁄2 atau m > 1⁄2
d. m > 1⁄2 atau m < - 1⁄2
e. m < -1⁄2 atau m > - 1⁄2
Pembahasan:
Perhatikan konsep berikut ini.
D > 0
4m² - 4m + 1 +8m > 0
4m² + 4m + 1 > 0
(2m + 1)² = 0
Jadi, himpunan penyelesaian pertidaksamaan tersebut adalah m < -1⁄2 atau m > - 1⁄2. Jawaban: E
2) Akar-akar persamaan kuadrat ax² - 3ax + 5(a-3) = 0 adalah x1 dan x2. Jika
(x1)3 dan (x2)3 = 117, maka a² + a sama dengan...
a. 4
b. 3
c. 2
d. 1
e. 0
Pembahasan:
ax² - 3ax + 5 (a - 3) = 0 → a = a; b = -3a; c = 5a - 15
maka diperoleh:
Contoh Soal Persamaan Kuadrat dan Jawaban Materinya Foto: Screenshoot
Substitusi persamaan (1) dan (ii) ke persamaan berikut.
(x1)3 dan (x2)3 = 117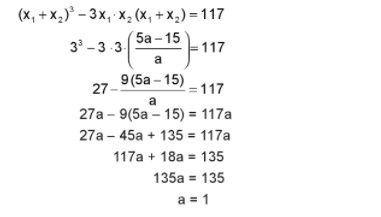
Contoh Soal Persamaan Kuadrat dan Jawaban Materinya Foto: Screenshoot
Dari hasil tersebut, maka
a² + a = 1² + 1
Jawaban C.
Itulah contoh soal persamaan kuadrat beserta pembahasannya. Selamat belajar detikers!
(pay/pay)
