Mengenal Rumus Deret Geometri, Contoh Soal, dan Penyelesaiannya

Dalam dunia matematika, deret geometri merupakan salah satu konsep yang sering dijumpai dalam berbagai bidang. Dengan memahami deret geometri, kita bisa menganalisis dan memecahkan berbagai masalah, seperti pertumbuhan populasi dan perhitungan investasi.

Deret geometri masih berkaitan dengan barisan geometri. Lantas, bagaimana rumus deret geometri? Berikut penjelasan beserta contoh soalnya.

Pengertian Deret Geometri

Deret geometri adalah jumlah suku-suku dari barisan geometri. Mengutip buku Matematika oleh Tri Dewi Listya dan Herawati, suatu barisan disebut dengan barisan geometri jika perbandingan dua suku yang berurutan selalu sama.

Contohnya, pada barisan 2, 4, 8, 16, 32,.. perbandingan dua suku berurutan pada barisan tersebut selalu sama, yaitu 4/2=8/4=16/8=32/16=2. Sehingga, barisan 2, 4, 8, 16, dan 32 adalah barisan geometri.

Menurut laman Kemdikbud, jika barisan geometrinya U₁, U₂, U₃,...U_n maka deret geometrinya adalah U₁+U₂+U₃+...+U_n.

Rumus Deret Geometri

Jumlah n suku pertama deret geometri dilambangkan dengan Sn. Nilai Sn dapat ditentukan dengan cara mengurangi persamaan 1 dan persamaan 2:

S_n = a+ar+ar2+...+ar^n-2+ar^n-1 (Persamaan 1)
rS_n= ar+ar²+...+ar^n-2+ar^n-1+arⁿ (Persamaan 2)

Hasilnya:

S_n-rS_n= a-arⁿ
(1-r)S_n= a (1-rⁿ), maka didapat rumus:

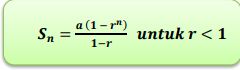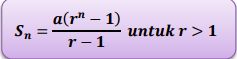Deret geometri Foto: (dok. Kemdikbud)

Deret geometri Foto: (dok. Kemdikbud)

Keterangan:

S_n= jumlah n suku pertama
a= suku pertama r=rasio/ pembanding
n=banyaknya suku

Contoh Soal Deret Geometri

Untuk memahami materi ini, kamu bisa melihat cara menyelesaikan soal deret geometri. Mengutip laman Kemdikbud dan Bank Soal UN Matematika SMA 2009 oleh Drs Sobirin, berikut beberapa contoh soal beserta penyelesaiannya.

1. Tentukan jumlah 10 suku pertama dari deret 3+6+12+...

Diketahui:

a=3
r=6/3=2 (r>1)

Pembahasan:

S_n=a(rⁿ-1)/r-1
S₁₀=3(2¹⁰-1)/2-1
= 3 (1024-1)/1
= 3. (1023)
= 3280

2. Suatu deret geometri 1+3+9+27+... tentukanlah

a. r dan U₈
b. Jumlah 8 suku yang pertama

Pembahasan:

a. r=3/1=3

U₈=ar^n-1
=1.3^8-1
= 3⁷
= 3280

b. S_n=a(rⁿ-1)/r-1
S₈= 1(3⁸-1)/3-1
= 6561-1/2
=3280

3. Produksi sebuah pabrik roti pada bulan pertama adalah 500 buah, jika produksi menurun 1/5 dari produksi sebelumnya, tentukan jumlah produksi pada bulan ke 5.

Diketahui:

a=500
r=400/500=4/5

Pembahasan:

U₅=a.r^n-1
=500 (4/5)^5-1

=500 (4/5)⁴

=500 (256/625)
=204,8 ≈ 205

Jadi, jumlah produksi pada bulan ke 5 adalah 205 roti.

4. Suku pertama dari deret geometri adalah 4 dan jumlah delapan suku pertama sama dengan tujuh belas kali jumlah empat suku pertama. Rasio deret geometri sama dengan:

Pembahasan:

S_n=a(rⁿ-1)/r-1
S₈=17 S₄
4(r⁸-1)/r-1=17 {4(r⁴-1)/r-1}
4(r⁴-1)(r+1)=(17).4.(4-1)
r⁴+1=17
r⁴=16
r=2

Video Trump Sebut Mahasiswa Tak Bisa Hitung 2+2 tapi Malah ke Harvard

Video Trump Sebut Mahasiswa Tak Bisa Hitung 2+2 tapi Malah ke Harvard