.webp)
Salah satu bangun datar yang dipelajari dalam Matematika, yaitu belah ketupat. Sama seperti bangun datar lain, belah ketupat memiliki ciri-ciri serta rumus tersendiri untuk menghitung keliling dan luasnya.
Untuk lebih mengenal bangun datar yang satu ini, simak ciri-ciri belah ketupat, rumus keliling dan luas, serta contoh soal dan pembahasannya pada uraian di bawah.
Apa Itu Belah Ketupat?
Mengutip buku Genius Matematika oleh Sulis Sutrisna, belah ketupat (rhombus) adalah bangun segi empat yang sisi-sisinya sama panjang. Sesuai namanya, bangun datar ini memiliki bentuk yang menyerupai ketupat.
SCROLL TO CONTINUE WITH CONTENT
Dilansir Cuemath, setiap belah ketupat termasuk jajar genjang, maka dari itu belah ketupat dikenal juga dengan jajar genjang khusus.
Hal ini karena bangun datar ini memenuhi syarat jajar genjang dengan segi empat yang memiliki 2 pasang sisi sejajar. Akan tetapi, bukan berarti semua jajar genjang adalah belah ketupat ya.
Ciri-ciri Belah Ketupat
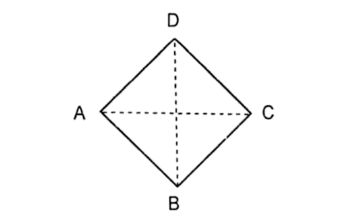 Belah Ketupat. Foto: Tangkapan layar dari buku Genius Matematika oleh Sulis Sutrisna |
Berikut ciri-ciri atau sifat-sifat belah ketupat:
- Keempat sisinya sama panjang → AB = BC = CD = AD
- Memiliki 2 pasang sisi berhadapan yang sejajar → AB // CD dan AD // BC
- Sudut yang berhadapan sama besar → ∠A = ∠C (berhadapan) dan ∠B = ∠D (berhadapan)
- Kedua diagonal saling berpotongan tegak lurus → AC ⟂ BD
- Garis diagonalnya membentuk 2 pasang segitiga kongruen dengan sudut 90°
- Diagonal belah ketupat merupakan sumbu simetri.
Rumus Belah Ketupat
Ada rumus yang dapat digunakan untuk menghitung keliling dan luas belah ketupat. Berikut rumus luas dan keliling belah ketupat:
Rumus Keliling Belah Ketupat
Karena keempat sisi belah ketupat sama panjang, maka rumusnya:
Keliling = 4 × sisi
Rumus Luas Belah Ketupat
Untuk menghitung luas belah ketupat, maka rumusnya:
Luas = ½ × diagonal₁ × diagonal₂
Atau
Luas = ½ × AC × BD
Contoh Soal Belah Ketupat dan Jawabannya
Agar lebih memahami bangun datar belah ketupat, cek beberapa contoh soal serta pembahasannya berikut ini.
Soal 1
Sebuah bangun datar mempunyai sifat-sifat berikut:
- Empat sisinya sama panjang dan sejajar
- Garis-garis diagonalnya berpotongan tegak lurus
- Sudut-sudut yang berhadapan sama besar.
Bangun ruang yang memiliki sifat-sifat di atas adalah...
A. Persegi
B. Jajar genjang
C. Layang-layang
D. Belah ketupat
Dan jawabannya adalah D. Belah ketupat.
Soal 2
Diketahui panjang sisi belah ketupat yaitu 13 cm. Berapakah kelilingnya?
Pembahasan:
Keliling = 4 × sisi
= 4 × 13 cm = 52 cm
Jadi, keliling belah ketupat adalah 52 cm.
Soal 3
Pada sebuah belah ketupat, diketahui: AC = 12 cm dan BD 12 cm. Hitunglah luas belah ketupat tersebut!
Pembahasan:
Luas = ½ × AC × BD
= ½ × 12 cm × 12 cm
= (½ × 12 × 12) cm² = 72 cm²
Jadi, luas belah ketupat tersebut adalah 72 cm².
Nah, itulah ciri-ciri belah ketupat beserta rumus keliling, rumus luas, contoh soal, dan pembahasannya.
(azn/inf)
