.webp)
Jika mempelajari matematika di kelas 7, kamu akan menemukan materi diagram venn. Bagi kamu yang belum tahu, diagram venn adalah gambar yang diimplementasikan untuk menyatakan sebuah himpunan.
Diagram Venn pertama kali diperkenalkan oleh seorang ahli matematika berkebangsaan Inggris yang hidup di tahun 1834-1923, John Venn. Bagaimana penyajian diagram venn? Apa saja bentuk-bentuk himpunannya? Berikut penjelasan beserta contoh soal mengenai diagram venn.
Apa Itu Diagram Venn?
Diagram venn adalah cara untuk menyampaikan himpunan dengan menggunakan gambar atau diagram. Himpunan adalah akumulasi dari variasi objek yang jelaskan secara sistematis dan terukur. Menurut buku Diagram Venn dan Operasinya oleh Tri Yulianto, Diagram Venn disajikan dengan cara sebagai berikut.
SCROLL TO CONTINUE WITH CONTENT
- Himpunan semesta digambarkan dengan persegi panjang dan diberi notasi S. S diletakkan di sudut kiri atas persegi panjang
- Himpunan yang dibicarakan digambarkan dengan lingkaran atau kurva tertutup lainnya.
- Setiap anggota himpunan dinyatakan dengan titik. Jika anggota himpunan sangat banyak titik-titikya tidak perlu digambar agar mudah dibaca.
Bentuk Diagram Venn
Bentuk diagram venn akan berkaitan dengan himpunan yang diwakilinya. Berikut beberapa bentuk diagram venn beserta contohnya.
1. Himpunan Berpotongan
Himpunan berpotongan adalah himpunan yang memiliki anggota satu sama lain. Misalnya:
P= {2, 3, 4, 5, 6} dan Q= {1, 3, 5, 7}
Menurut buku Rangkuman Penting Intisari 4 Mata Pelajaran Utama SMP oleh Sukma Pratiwi, S.Pd, P~Q dan Q~P. Himpunan P dan Q memiliki anggota yang sama, yaitu 3 dan 5.
2. Himpunan Saling Lepas
Himpunan saling lepas kebalikan dari himpunan berpotongan. Himpunan dikatakan saling lepas jika irisannya kosong. Misalnya:
A= {1, 2, 3, 4}
B= (r, s, t}
Jadi, A dan B saling lepas, atau ditulis dengan A//B
3. Himpunan Sama
Himpunan A dan B dikatakan sama jika semua anggotanya sama. Misalnya:
A={2, 4, 6}
B={6, 4, 2}
Himpunan sama ditulis dengan A=B
4. Himpunan Bagian
Himpunan bagian adalah ketika seluruh anggota himpunan berada di himpunan lain. Misalnya:
A={13, 15, 17}
B={13, 14, 15, 16, 17}
Jadi, himpunan A merupakan bagian dari himpunan B. A ⊂ B, sebab anggota A merupakan anggota B.
Contoh Soal Diagram Venn
Agar lebih paham, berikut beberapa contoh soal dari diagram venn. Mengutip buku Buku Rumus Pintar Matematika oleh Sandy Fahamsyah, buku Mari Memahami Konsep Matematika oleh Wahyudin Jumanta, dan buku Diagram Venn dan Operasinya oleh Tri Yulianto berikut penjelasannya.
1. Diketahui:
- S adalah himpunan bilangan cacah kurang dari 10
- A adalah himpunan bilangan cacah ganjil kurang dari 10
Dengan mengambil S sebagai himpunan semesta, buatlah diagram venn untuk himpunan-himpunan ini.
Jawab:
S adalah himpunan bilangan cacah kurang dari 10
Jadi, S= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A adalah himpunan bilangan cacah ganjil kurang dari 10
Jadi, A= {1, 3, 5, 7, 9}
Berikut langkah membuat diagram venn:
1. Buat persegi panjang dengan himpunan semesta (S). Tulis notasi S di pojok kiri atas
 Diagram venn Foto: Buku Diagram Venn dan Operasinya oleh Tri Yulianto |
2. Buat lingkaran atau elips yang mewakili himpunan A. Di atas lingkaran, tulis A yang menyatakan bahwa lingkaran itu mewakili himpunan A
3. Anggota himpunan A adalah 1, 3, 5, 7, dan 9. Buat titik sebanyak lima buah di dalam lingkaran
4. Di dekat masing-masing titik, tulis kelima anggota himpunan A
5. Kemudian, pilih anggota himpunan S yang tidak termasuk dalam anggota A.
Anggota himpunan S adalah 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Sehingga anggota himpunan S yang tidak termasuk anggota himpunan A adalah 0, 2, 4, 6, dan 8.
6. Buat lima titik pada persegi panjang untuk mewakili himpunan S di luar lingkaran yang mewakil himpunan A.
7. Di dekat masing-masing titik, tulis anggota himpunan S yang tidak termasuk anggota himpunan A, yaitu 0, 2, 4, 6, dan 8.
8. Diagram venn pun telah selesai dibuat.
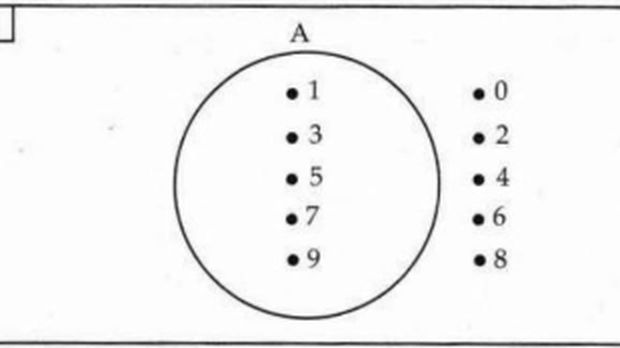 Diagram venn Foto: Buku Diagram Venn dan Operasinya oleh Tri Yulianto |
2. Diketahui:
- S adalah himpunan bilangan cacah yang kurang dari atau sama dengan 12
- L adalah himpunan bilangan ganjil kurang dari 12
- P adalah himpunan bilangan prima kurang dari 12
Gambarkan Diagram Venn untuk menyatakan ketiga himpunan tersebut.
Jawab:
S= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
L= {1, 3, 5, 7, 9, 11}
P={2, 3, 5, 7, 11}
Sehingga, bentuk Diagram Vennnya adalah sebagai berikut:
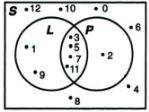 Diagram venn Foto: Buku Rumus Pintar Matematika oleh Sandy Fahamsyah |
Angka yang berada di tengah merupakan himpunan yang sama antara S, L dan P. Sementara angka yang berada di luar lingkaran adalah milik himpunan S.
3. Diketahui:
- S= {a, b, c, d, e, f, g}
- A={a, b, c}
- B={d, e, f}
Buatlah diagram venn dari himpunan di atas!
Jawab:
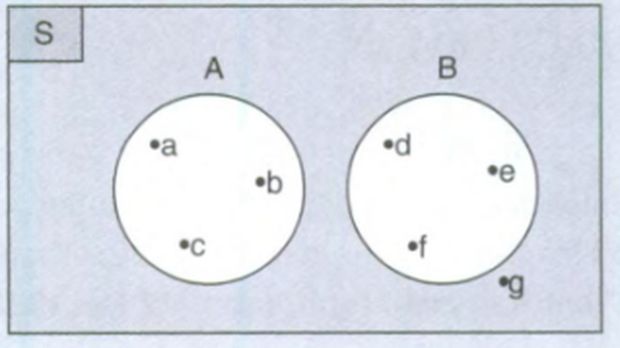 Diagram venn Foto: Buku Rumus Pintar Matematika oleh Sandy Fahamsyah |
Itulah penjelasan mengenai diagram venn. Semoga kamu bisa memahami materi ini ya.
(elk/row)
