.webp)
Balok merupakan salah satu bangun ruang yang memiliki panjang, lebar, dan tinggi. Sifat yang dimiliki balok yaitu memiliki 6 sisi persegi panjang, 12 rusuk, dan 8 titik sudut. Setiap bangun ruang dapat diketahui luas permukaan dan juga volumenya.
Lantas, apa rumus luas permukaan balok? Simak penjelasannya berikut ini.
Ciri-Ciri Balok
Dikutip dari buku berjudul Asyiknya Belajar Bangun Ruang dan Sisi Datar yang ditulis oleh Nur Laila Indah Sari, berikut ini ciri-ciri yang dimiliki oleh balok:
SCROLL TO CONTINUE WITH CONTENT
- Memiliki 6 bidang sisi berbentuk persegi panjang
- Memiliki 12 rusuk. Rusuk-rusuk yang sejajar berukuran sama panjang
- Setiap diagonal bidang pada sisi yang berhadapan berukuran sama panjang
- Memiliki 8 titik sudut
- Seluruh sudut balok berbentuk siku-siku
- Terdapat 4 diagonal ruang dan 12 diagonal bidang
- Setiap diagonal ruang berukuran sama panjang
- Setiap diagonal memiliki bentuk persegi panjang.
Rumus Luas Permukaan Balok
Dikutip dari buku berjudul TOP No. 1 UN SMP/MTs 2016 Seri Pendalaman Materi yang ditulis oleh Tim Guru Indonesia, berikut ini rumus luas permukaan balok:
- L = 2 x [(p x l) + (p x t) + (l x t)]
Keterangan:
L = luas permukaan balok
p = panjang balok
l = lebar balok
t = tinggi balok
6 Contoh Soal Luas Permukaan Balok
Dikutip dari buku berjudul Matematika untuk SMP dan MTs Kelas VIII yang ditulis oleh Budi Suryatin, dkk. Berikut ini 5 contoh soal luas permukaan balok agar kamu lebih memahaminya:
1. Jika panjang rusuk balok mainan milik Sinta AB = 20 cm, BC = 10 cm, dan BF = 5 cm. Maka, berapa luas permukaan balok tersebut?
Jawab:
L = 2 x [(p x l) + (p x t) + (l x t)]
= 2 x [(20 x 10) + (20 x 5) + (10 x 5)]
= 2 (200 + 100 + 50)
= 2 (350)
= 700 cm²
2. Sebuah balok memiliki panjang 18 cm, lebar 12 cm, dan tinggi 9 cm. Luas permukaan balok tersebut adalah...
Jawab:
L = 2 x [(p x l) + (p x t) + (l x t)]
= 2 x [(18 x 12) + (18 x 9) + (12 x 9)
= 2 (216 + 162 + 108)
= 2 (486)
= 972 cm²
3. Luas Permukaan bangun disamping adalah...
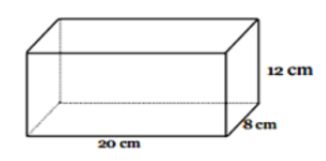 Balok. Foto: Modul USBN SD/MI Tahun 2019 oleh Usman Jayadi |
Jawab:
L = 2 x [(p x l) + (p x t) + (l x t)]
= 2 x [(20 x 8) + (20 x 12) + (8 x 12)
= 2 (160 + 240 + 96)
= 2 (496)
= 992 cm²
4. Sebuah balok memiliki lebar 5 cm dan tinggi 3 cm. Jika luas permukaannya adalah 142 cm², berapa panjang balok tersebut?
Jawab:
L = 2 x [(p x l) + (p x t) + (l x t)]
142 = 2 x [(p x 5) + (p x 3) + (5 x 3)]
142 = 2 (5p + 3p + 15)
142 = 2 (8p + 15)
142/2 = 8p + 15
71 = 8p + 15
71 - 15 = 8p
56 = 8p
p = 7 cm
5. Diketahui volume sebuah balok adalah 1.000 cm³. Jika panjang balok adalah 20 cm dan tingginya 5 cm. Berapa luas permukaan balok tersebut?
Jawab:
l = V/(pxt)
l = 1.000/ 20 x 5
l = 1.000/100
l = 10 cm
L = 2 x [(p x l) + (p x t) + (l x t)]
= 2 x [(20 x 10) + (20 x 5) + (10 x 5)]
= 2 x (200 + 100 + 50)
= 2 x (350)
= 700 cm²
6. Diketahui volume suatu balok adalah 300 cm³. Jika tinggi balok adalah 5 cm dan lebarnya adalah 6 cm. Berapa luas permukaan balok?
Jawab:
p = V/(lxt)
p = 300/(5x6)
p = 300/30
p = 10 cm
L = 2 x [(p x l) + (p x t) + (l x t)]
= 2 x [(10 x 6) + (10 x 5) + (6 x 5)
= 2 (60 + 50 + 30)
= 2 (140)
= 280 cm²
Demikian penjelasan tentang rumus luas permukaan balok. Semoga bisa membantu detikers belajar ya.
(row/row)
