Sudut Istimewa Trigonometri pada Setiap Kuadran Beserta Contoh Soalnya

Trigonometri adalah salah satu materi pada mata pelajaran Matematika yang mempelajari tentang hubungan antara panjang sudut dengan sebuah segitiga. Dalam trigonometri, dikenal dengan tiga istilahnya, yaitu sinus (sin), cosinus (cos), dan tangen (tan). Dalam trigonometri, dikenal juga istilah sudut istimewa.

Apa kira-kira sudut istimewa itu? Berikut ini penjelasan lengkapnya mengenai sudut istimewa mulai dari kuadran I sampai dengan kuadran IV, beserta contoh-contoh soal untuk membantu melatih pemahaman.

Pengertian Sudut Istimewa

Dikutip melalui buku berjudul Matematika karya M. Farid Nasrulloh, dkk (2023), sudut istimewa adalah suatu sudut, yang di aman nilai dari perbandingan trigonometrinya bisa ditentukan langsung tanpa perlu menggunakan daftar trigonometri ataupun bantuan kalkulator.

Sederhananya, sudut istimewa dapat mengungkapkan langsung rasio dari panjang sisi pada setiap sudut tertentu. Sudut yang dimaksud adalah sudut dengan besaran 0°, 30°, 45°, 60°, dan 90°. Dalam matematika, perbandingan antara sisi dan sudut dihitung dengan menggunakan istilah sin, cos, tan, cosec, sec, dan cotan.

Berikut ini tabel sudut istimewa trigonometri:

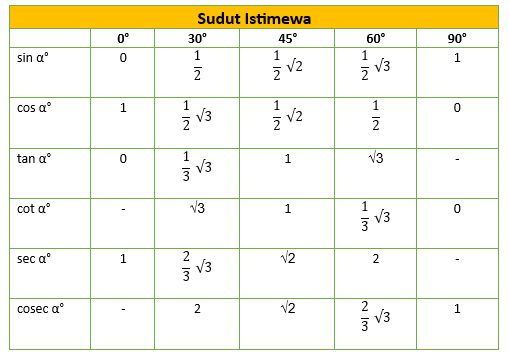Foto: Rindang Krisnawati/detikcom

Melalui tabel sudut istimewa trigonometri di atas, bisa disimpulkan bahwa:

1. tan α = sin α / cos α
2. sec α = 1 / cos α
3. cosec α = 1 / sin α
4. cotan α = 1 / tan α.

Sudut Istimewa Berelasi

Berikut ini sudut-sudut berelasi dikutip melalui buku berjudul Contekan Rumus Matematika karya Bagus Sulasmono (2009).

Sudut Istimewa Kuadran I

Sudut istimewa kuadran I terletak di antara sudut 0° sampai dengan sudut 90°. Pada kuadran I, semua nilai dari trigonometri memiliki nilai positif. Berikut ini perbandingan trigonometri untuk sudut istimewa yang ada di kuadran I.

1. 0° = sin 0, cos 1, tan 0
2. 30° = sin 1/2, cos 1/2 √3, tan 1/3 √3
3. 45° = sin 1/2 √2, cos 1/2 √2, tan 1
4. 60° = sin 1/2 √3, cos 1/2, tan √3
5. 90° = sin 1, cos 0, tan ~.

Rumus perbandingan trigonometrinya (90 - α)°:

1. sin (90 - α)° = cos α°
2. cos (90 - α)° = sin α°
3. tan (90 - α)° = cotan α°
4. cosec (90 - α)° = sec α°
5. sec (90 - α)° = cosec α°
6. cotan (90 - α)° = tan α°.

Sudut Istimewa Kuadran II

Sudut istimewa kuadran II terletak di antara sudut 90° sampai dengan sudut 180° Pada kuadran II, semua nilai dari trigonometri juga akan memiliki nilai positif. Sedangkan untuk cosinus dan tangen bernilai negatif. Berikut ini perbandingan trigonometri untuk sudut istimewa yang ada di kuadran II.

1. 90° = sin 1, cos 0, tan tidak terdefinisi
2. 120° = sin 1/2 √3, cos -1/2, tan -√3
3. 135° = sin 1/2 √2, cos -1/2 √2, tan -1
4. 150° = sin 1/2, cos -1/2 √3, tan -1/3 √3
5. 180° = sin 0, cos -1, tan 0.

Rumus perbandingan trigonometrinya (180 - α)°:

1. sin (180 - α)° = sin α°
2. cos (180 - α)° = -cos α°
3. tan (180 - α)° = -tan α°
4. cosec (180 - α)° = cosec α°
5. sec (180 - α)° = -sec α°
6. cotan (180 - α)° = -cotan α°.

Sudut Istimewa Kuadran III

Sudut istimewa kuadran III terletak di antara sudut 180° sampai dengan sudut 270°. Pada kuadran III, hanya tangen saja yang bernilai positif, sisanya bernilai negatif. Berikut ini perbandingan trigonometri untuk sudut istimewa yang ada di kuadran III.

1. 180° = sin 0, cos -1, tan 0
2. 210° = sin -1/2, cos -1/2 √3, tan 1/3 √3
3. 225° = sin -1/2 √2, cos -1/2 √2, tan 1
4. 240° = sin -1/2 √3, cos -1/2, tan √3
5. 270° = sin -1, cos 0, tan tidak terdefinisi.

Rumus perbandingan trigonometrinya (180 + α)°:

1. sin (180 + α)° = -sin α°
2. cos (180 + α)° = -cos α°
3. tan (180 + α)° = tan α°
4. cosec (180 + α)° = -cosec α°
5. sec (180 + α)° = -sec α°
6. cotan (180 + α)° = cotan α°.

Sudut Istimewa Kuadran IV

Sudut istimewa kuadran IV terletak di antara sudut 270° sampai dengan sudut 360°. Pada kuadran IV, hanya cosinus saja yang memiliki nilai positif. Sedangkan sisanya bernilai negatif. Berikut ini perbandingan trigonometri untuk sudut istimewa yang ada di kuadran IV.

1. 270° = sin -1, cos 0, tan tidak terdefinisi
2. 300° = sin-1/2 √3, cos 1/2, tan -√3
3. 315° = sin -1/2 √2, cos 1/2 √2, tan -1
4. 330° = sin -1/2, cos 1/2 √3, tan -1/3 √3
5. 360° = sin 0, cos 1, tan 0.

Rumus perbandingan trigonometrinya (360-α)°:

1. sin (360 - α)° = -sin α°
2. cos (360 - α)° = cos α°
3. tan (360 - α)° = -tan α°
4. cosec (360 - α)° = cosec α°
5. sec (360 - α)° = sec α°
6. cotan (360 - α)° = -cotan α°.

Contoh Soal Sudut Istimewa Trigonometri

1. Hitunglah sudut istimewa tan 60° + tan 45°
Pembahasan:
Diketahui:
tan 60° = √3
tan 45° = 1

tan 60° + tan 45°
= √3 + 1

2. Hitunglah sudut istimewa sin 90° - sin 45°
Pembahasan:
Diketahui:
sin 90° = 1
sin 45° = 1/2 √2

sin 90° - sin 45°
= 1 - 1/2 √2
= -1/2 (√2 + 2)

3. Hitunglah sudut istimewa tan 30° + tan 45°
Pembahasan:
Diketahui:
tan 30° = 1/3 √3
tan 45° = 1

tan 30° + tan 45°
= 1/3 √3 + 1
= 1/3 (√3 + 3)

4. Tunjukkan apa benar sin² 45° + cos² 45° = 1
Pembahasan:
Diketahui:
sin 45° = 1/2 √2
cos 45° = 1/2 √2

Maka:

sin² 45° + cos² 45° = 1
(1/2 √2)² + (1/2 √2)² = 1
1/2 + 1/2 = 1

Persoalan tersebut juga bisa diselesaikan menggunakan identitas trigonometri, yaitu:
sin² x + cos² x = 1

Demikian yang dapat detikEdu sampaikan mengenai sudut istimewa mulai dari kuadran I hingga kuadran IV. Semoga bermanfaat!

Video: Sosok Pria Bali Bikin Seruling Pakai Rumus Fisika hingga Geometri

Video: Sosok Pria Bali Bikin Seruling Pakai Rumus Fisika hingga Geometri