Bagi kamu yang duduk di bangku sekolah, pasti sudah tidak asing dengan bangun datar segitiga dalam pelajaran matematika. Tentu kamu pernah diberi tugas oleh guru untuk menghitung tinggi segitiga, bukan?
Tinggi segitiga adalah ruas garis tegak lurus yang ditarik dari titik sudut segitiga ke sisi yang berhadapan dengannya. Tinggi segitiga membentuk sudut siku-siku dengan alasnya.
Lantas, bagaimana cara menghitung tinggi segitiga? Berikut ini beberapa rumus tinggi segitiga yang perlu kamu ketahui.
SCROLL TO CONTINUE WITH CONTENT
Rumus Tinggi Segitiga
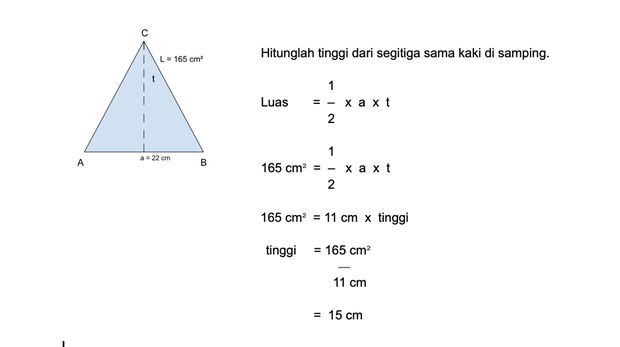 Contoh soal segitiga sama kaki. Foto: Khadeshia Marsha/detikcom Contoh soal segitiga sama kaki. Foto: Khadeshia Marsha/detikcom |
Rumus tinggi segitiga dapat berbeda-beda tergantung aspek apa yang diketahui dalam soal. Misalnya, rumus tinggi segitiga jika diketahui luas dan alasnya tentu berbeda dengan rumus tinggi segitiga apabila diketahui alas dan sisi miringnya.
Selain itu, rumus tinggi segitiga juga bisa berbeda tergantung dari jenis segitiga. Misalnya, rumus tinggi segitiga siku-siku berbeda dengan rumus segitiga saa sisi.
Nah, berikut ini rumus-rumus tinggi segitiga.
1. Rumus tinggi segitiga jika diketahui luas dan alasnya
Dikutip dari buku Ringkasan Matematika SD: Panduan Lengkap dan Praktis oleh Ir. Koeshartati Saptorini, rumus segitiga jika diketahui luas dan alasnya adalah sebagai berikut.
- tinggi = (2 x luas segitiga) : alas
Contoh soal:
Suatu segitiga mempunyai luas 20 cm². Jika panjang alasnya 5 cm, tentukan tinggi segitiga tersebut!
Jawab:
tinggi = (2 x luas segitiga) : alas
tinggi = (2 x 20) : 5
tinggi = 8
Jadi, tinggi segitiga tersebut adalah 8 cm.
2. Rumus tinggi segitiga siku-siku
Menghitung tinggi segitiga siku-siku dapat berpedoman pada teorema pythagoras. Mengutip dari buku Rumus Lengkap Matematika SMP oleh Drs. Joko Untoro, rumus pythagoras adalah:
- c² = a² + b²
Rumus pythagoras sebenarnya digunakan untuk mencari sisi terpanjang segitiga, apabila alas dan tingginya sudah diketahui. Namun, kamu juga bisa menggunakan rumus ini untuk mencari tinggi segitiga siku-siku.
Untuk mencari tinggi segitiga siku-siku, ini adalah rumus yang bisa kamu gunakan:
b² = c² - a² atau b = √[c² - a²]
- b = tinggi segitiga
- a = panjang alas segitiga
- c = panjang sisi miring atau sisi terpanjang segitiga.
Contoh Soal:
Sebuah segitiga siku-siku memiliki alas 60 cm dan sisi miring 61 cm. Berapa tinggi segitiga tersebut?
Jawab:
b = √[c² - a²]
b = √[61² - 60²]
b = √[3721 - 3600]
b = √121
b = 11
Jadi, tinggi segitiga tersebut adalah 11 cm.
3. Rumus tinggi segitiga jika diketahui alas dan sisi miringnya
Apabila suatu segitiga diketahui alas dan sisi miringnya, maka tinggi segitiga juga dapat dicari menggunakan teorema Pythagoras. Ini karena alas, tinggi, dan sisi miring segitiga dapat membentuk segitiga siku-siku yang memenuhi persamaan Pythagoras.
Dengan demikian, rumus tinggi segitiga jika diketahui alas dan sisi miringnya adalah:
- b² = c² - a² atau b = √[c² - a²]
b = tinggi segitiga
a = panjang alas segitiga
c = panjang sisi miring atau sisi terpanjang segitiga
Contoh Soal:
Diketahui sebuah segitiga memiliki alas 35 cm dan sisi miring 37 cm. Tentukan tinggi segitiga tersebut!
Jawab:
b = √[c² - a²]
b = √[35² - 37²]
b = √[1225 - 1369]
b = √144
b = 12
Jadi, tinggi segitiga tersebut adalah 12 cm.
4. Rumus tinggi segitiga sama sisi
Segitiga sama sisi memiliki 3 sisi yang sama panjang. Jika segitiga sama sisi dibagi menjadi dua, maka kamu akan mendapatkan dua segitiga siku-siku yang kongruen atau sama besar.
Sebab itu, kamu dapat menggunakan teorema pythagoras untuk mencari tinggi segitiga sama sisi. Adapun rumus yang dapat kamu gunakan adalah:
- b² = c² - (1/2 x a)² atau b = √[c² - (1/2 x a)²]
b = tinggi segitiga
a = panjang alas segitiga
c = panjang sisi miring atau sisi terpanjang segitiga
Contoh soal:
Diketahui sebuah segitiga sama sisi memiliki sisi 8cm. Tentukan tinggi dari segitiga sama sisi tersebut!
Jawab:
Segitiga sama sisi mempunyai 3 sisi yang sama panjang, maka diketahui alas = 8 cm dan sisi miring = 8 cm
b = √[c² - (1/2 x a)²]
b = √[8² - (1/2 x 8)²]
b = √[8² - 4²]
b = √[64-16]
b = √48
b = 6,93
Jadi, tinggi segitiga sama sisi tersebut adalah 6,93 cm
Nah, itulah beberapa rumus tinggi segitiga yang perlu kamu ketahui. Semoga bermanfaat dan selamat belajar, detikers.
(row/row)


























































