Persamaan Lingkaran dan Contoh Soalnya

Pada pelajaran mata matematika, detikers pasti telah mempelajari tentang bangun datar. Salah satu bentuk dari bangun datar adalah lingkaran. Lingkaran memiliki beberapa konsep, seperti keliling, luas, luas juring, panjang tali busur, persamaan lingkaran, dan lain-lain.

Persamaan lingkaran dipelajari pada mata pelajaran Matematika Peminatan SMA Kelas XI. Persamaan lingkaran memiliki beberapa rumus berdasarkan titik lingkaran.

Yuk simak penjelasan tentang rumus persamaan lingkaran dan contoh soalnya.

Pengertian dan Unsur Lingkaran

Dikutip dari buku Pasti Bisa Matematika untuk SMP/MTs Kelas VIII (2018), lingkaran adalah sekumpulan titik-titik yang tidak terhingga dan memiliki jarak yang sama pada satu titik tertentu. Titik tertentu tersebut adalah titik pusat lingkaran O dan jaraknya disebut dengan jari-jari.

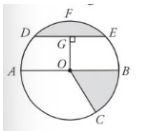Lingkaran. Foto: Pasti Bisa Matematika untuk SMP/MTs Kelas VIII/Tim Ganesha Operation.

Keterangan:

• O : titik pusat
• OA = OB : jari-jari lingkaran (r)
• AB : diameter atau D = OA + OB = 2r
• BC : busur lingkaran
• BOC : juring lingkaran
• DE : tali busur
• DFE : tembereng
• OG : jarak O pada DE disebut juga sebagai apotema

Rumus Persamaan Lingkaran

Dikutip dari buku berjudul Strategi Praktis Menguasai Tes Matematika SMA Kelas 2 IPA yang ditulis oleh Drs. Sobirin, berikut konsep persamaan lingkaran:

1. Persamaan lingkaran yang berpusat di titik O (0,0) dan jari-jari r sebagai berikut.

x² + y² = r²

2. Persamaan lingkaran yang berpusat di (a, b) dan jari-jari r sebagai berikut.

(x - a)² + (y - b)² = r²

3. Persamaan Umum lingkaran

Persamaan Umum Lingkaran = x² + y² + Ax + By + C = 0

Pusatnya = P = (- ½ A. - ½ B)

Jari-jari r = √¼ A² + ¼ B² - C

4. Persamaan Lingkaran dengan Kriteria Tertentu

Terdapat dua cara untuk menentukan persamaan lingkaran, yaitu:

a. Menentukan pusat dan jari-jari, lalu substitusikan ke dalam persamaan

(x - a)² + (y - b)² = r

b. Menentukan nilai A, B, C. Lalu substitusikan ke persamaan

x² + y² + Ax + By + C = 0

Contoh Soal Persamaan Lingkaran

Dikutip dari Modul Pembelajaran Matematika Peminatan Kelas XI (2020), berikut contoh soal persamaan lingkaran:

1. Tentukan persamaan lingkaran yang berpusat di O(0, 0) dan memiliki jari-jari sebagai berikut.

a. r = 4

b. r = 4√3

Jawab:

Persamaan lingkaran yang berpusat di lingkaran O(0, 0) dan berjari-jari r adalah x² + y² = r²

a. Diketahui r = 4, dengan persamaan x² + y² = r²

x² + y² = r²
x² + y² = 4²
x² + y² = 16

b. Diketahui r = 4√3, dengan persamaan x² + y² = r²

x² + y² = r²
x² + y² = (4√3)²
x² + y² = 48

2. Tentukan persamaan lingkaran

a. berpusat di (4, -5) dengan jari-jari 6.

b. berpusat di (-2, -6) dan memiliki jari-jari 3√2

Jawab:

a. Titik pusat lingkaran (4, -5) dan jari-jari 6, maka persamaannya adalah

(x - a)² + (y - b)² = r²
(x - 4)² + (y - (-5))² = 6²
(x - 4)² + (y + 5)² = 36

b. Titik pusat lingkaran (-2, -6) dan jari-jari r = 3√2, maka persamaannya adalah

(x - a)² + (y - b)² = r²
(x - (-2))² + (y - (-6))² = (3√2)²
(x + 2)² + (y + 6)² = 18

3. Tulis persamaan umum lingkaran yang berpusat di M(-4, 3) dengan jari-jari 7.

Jawab:

Pusat (-4, 3) dan r = 7, maka persamaannya:

(x - a)² + (y - b)² = r²
(x - (-4))² + (y - 3)² = 7²
(x + 4)² + (y - 3)² = 49
x² + 8x + 16 + y² - 6y + 9 = 49
x² + y² + 8x - 6y - 24 + 0

Atau dengan menentukan A = -2a, B = -2b, dan C = a² + b² - r² diperoleh

A = -2(-4) = 9
B = -2(3) = -6
C = (-4)² + 3² - 7² = 16 + 9 - 49 = -24

Maka persamaan lingkarannya adalah x² + y² + 8x - 6y - 24 = 0

4. Tentukan persamaan lingkaran yang berpusat di O(0, 0) dan menyinggung garis 3x - 4y + 5 = 0

Jawab:

Untuk menentukan persamaan lingkaran, kita harus mencari nilai r terlebih dahulu.

Jarak sembarang titik (x1, y1) ke garis Ax + By + C = 0 adalah

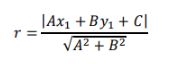Persamaan lingkaran. Foto: Modul Pembelajaran Matematika Peminatan Kelas XII/Kemendikbud.

Jarak antara titik O(0,0) dengan garis 3x - 4y + 5 = 0 adalah:

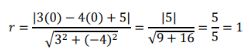Persamaan lingkaran. Foto: Modul Pembelajaran Matematika Peminatan Kelas XII/Kemendikbud.

Jadi persamaan lingkaran yang berpusat di O(0, 0) dan menyinggung garis 3x - 4y + 5 = 0 adalah x² + y² = 1

5. Tentukan pusat dan jari- jari lingkaran dengan persamaan x² + y² + 2ax + 2by - 2ab = 0

Jawab:

Dari persamaan di atas diperoleh:

A = 2a, B = -2b, dan C = -2ab

- Pusat (- ½ A, - ½ B) = (-a,b)

- jari-jari = r

= √(-½ A)² + (-½ B)² - C
= √(-a)² + (b)² - (-2ab)
= √a² + b² - 2ab
= √(a + b)²
= (a + b)

Demikian penjelasan tentang persamaan lingkaran. Semoga bermanfaat.

Video Trump Sebut Mahasiswa Tak Bisa Hitung 2+2 tapi Malah ke Harvard

Video Trump Sebut Mahasiswa Tak Bisa Hitung 2+2 tapi Malah ke Harvard