Rumus kuartil digunakan untuk mencari letak data yang telah dibagi menjadi empat bagian.
Ketahui apa itu kuartil, lengkap dengan rumus kuartil untuk data tunggal dan berkelompok, serta contoh soalnya.
Pengertian Kuartil
Sebelum mengetahui rumus kuartil, kita terlebih dahulu harus mengetahui pengertian kuartil. Berdasarkan buku Statistika Matematika Umum Kelas XII Kemdikbud, kuartil adalah ukuran letak yang membagi data yang sudah diurutkan menjadi empat bagian sama banyak.
SCROLL TO CONTINUE WITH CONTENT
Karena dibagi menjadi empat bagian, maka ada tiga bagian pemisah, yaitu kuartil 1 atau kuartil bawah (Q1), kuartil 2 atau kuartil tengah (Q2), dan kuartil 3 atau kuartil atas (Q3). Q1 berada di antara bagian pertama dan kedua, Q2 berada di antara bagian kedua dan ketiga, serta Q3 berada di antara bagian ketiga dan keempat.
Rumus Kuartil Data Tunggal
Rumus kuartil dibedakan menjadi dua. Pertama untuk menghitung data tunggal, dan kedua untuk menghitung data berkelompok. Data tunggal masih dibedakan lagi menjadi data ganjil dan genap.
Data tunggal adalah data statistik yang satu nilainya mewakili satu frekuensi. Rumusnya berbeda antara data berjumlah ganjil dan genap.
Data Ganjil Jika n+1 Habis Dibagi 4
Rumus menghitung kuartil data tunggal ganjil jika n+1 habis dibagi 4 adalah sebagai berikut:
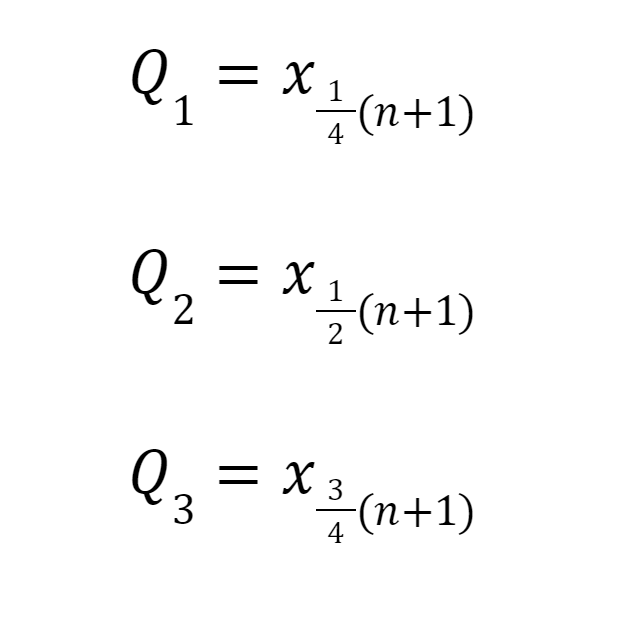 Data Kuartil Ganjil Jika n+1 Habis Dibagi 4. Foto: Bayu Ardi Isnanto/detikcom Data Kuartil Ganjil Jika n+1 Habis Dibagi 4. Foto: Bayu Ardi Isnanto/detikcom |
Data Ganjil Jika n+1 Tidak Habis Dibagi 4
Rumus menghitung kuartil data tunggal ganjil jika n+1 tidak habis dibagi 4 adalah sebagai berikut:
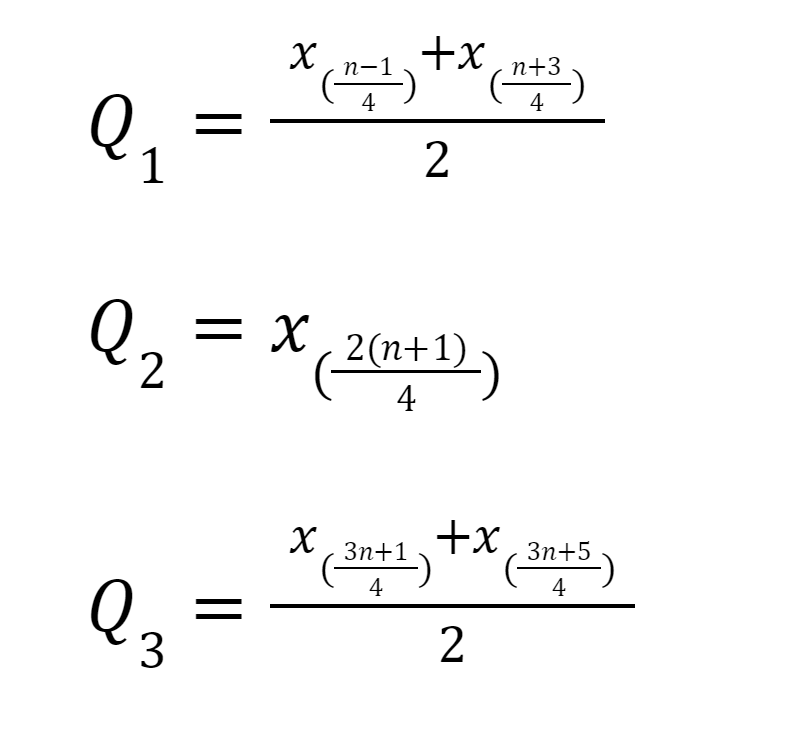 Data Ganjil Jika n+1 Tidak Habis Dibagi 4 Foto: Bayu Ardi Isnanto/detikcom Data Ganjil Jika n+1 Tidak Habis Dibagi 4 Foto: Bayu Ardi Isnanto/detikcom |
Data Genap Jika n Habis Dibagi 4
Rumus menghitung kuartil data tunggal genap jika n habis dibagi 4 adalah sebagai berikut:
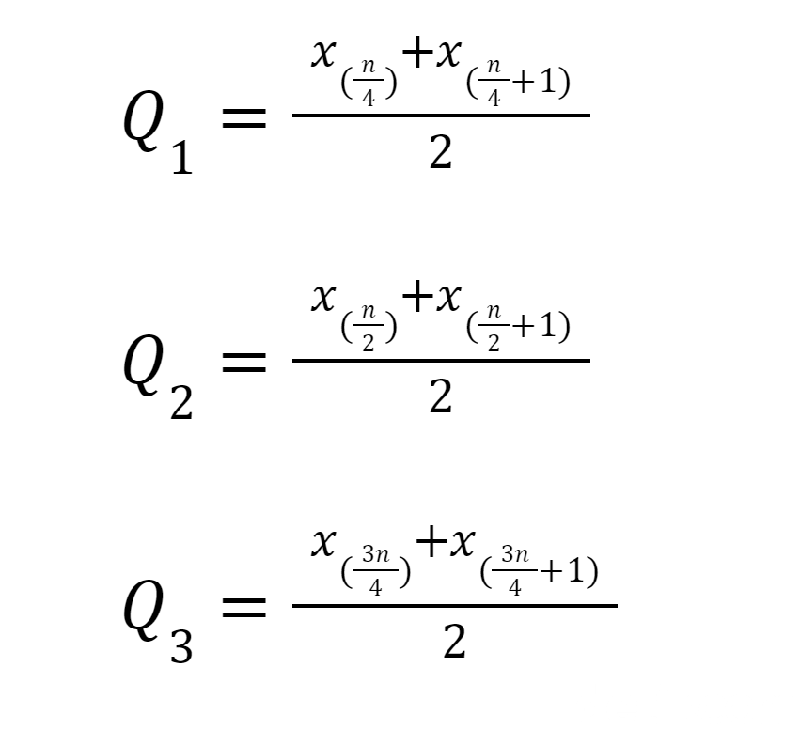 Data Genap Jika n Habis Dibagi 4. Foto: Bayu Ardi Isnanto/detikcom Data Genap Jika n Habis Dibagi 4. Foto: Bayu Ardi Isnanto/detikcom |
Data Genap Jika n Tidak Habis Dibagi 4
Rumus menghitung kuartil data tunggal genap jika n tidak habis dibagi 4 adalah sebagai berikut:
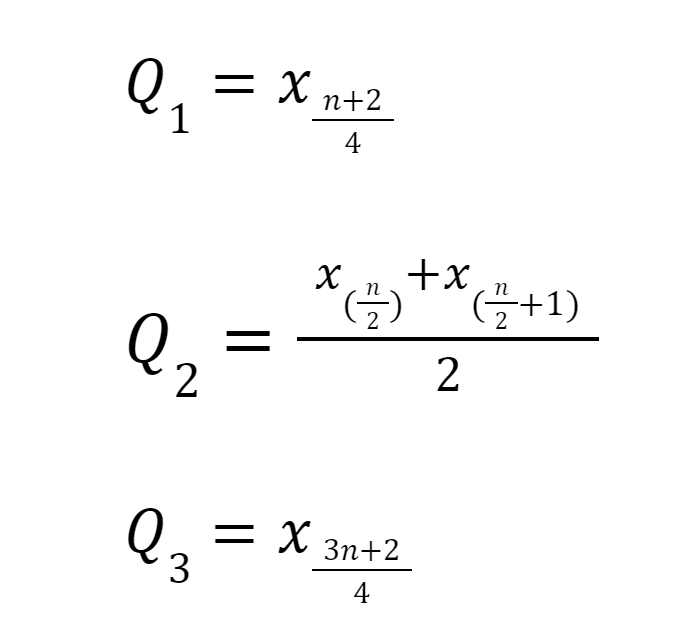 Data Genap Jika n Tidak Habis Dibagi 4. Foto: Bayu Ardi Isnanto/detikcom Data Genap Jika n Tidak Habis Dibagi 4. Foto: Bayu Ardi Isnanto/detikcom |
Rumus Kuartil Data Berkelompok
Berbeda dengan data tunggal, data statistik berkelompok memiliki nilai dengan interval tertentu. Misal: nilai 11-20 memiliki frekuensi 29, nilai 21-30 memiliki frekuensi 32, dan seterusnya.
Maka rumus kuartilnya adalah sebagai berikut:
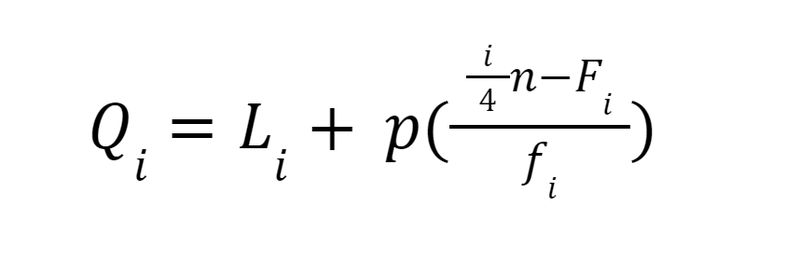 Rumus Kuartil Data Berkelompok. Foto: Bayu Ardi Isnanto/detikcom Rumus Kuartil Data Berkelompok. Foto: Bayu Ardi Isnanto/detikcom |
Keterangan:
Qi = Kuartil ke-i
Li = Tepi bawah kelas kuartil ke-i dikurangi 0,5
p = panjang kelas interval
Fi = frekuensi kumulatif tepat sebelum kelas kuartil ke-i
fi = frekuensi kelas kuartil ke-i
n = banyak datum
Contoh Soal
Agar lebih paham dalam menerapkan rumus kuartil, cobalah berlatih dengan contoh-contoh soal berikut ini.
Contoh 1
Jika datanya berjumlah ganjil dengan n+1 yang habis dibagi 4, contohnya sebagai berikut:
4, 4, 5, 7, 8, 8, 8, 9, 10, 11, 11
Dari contoh data di atas, kita akan coba cari Q1, Q2, dan Q3.
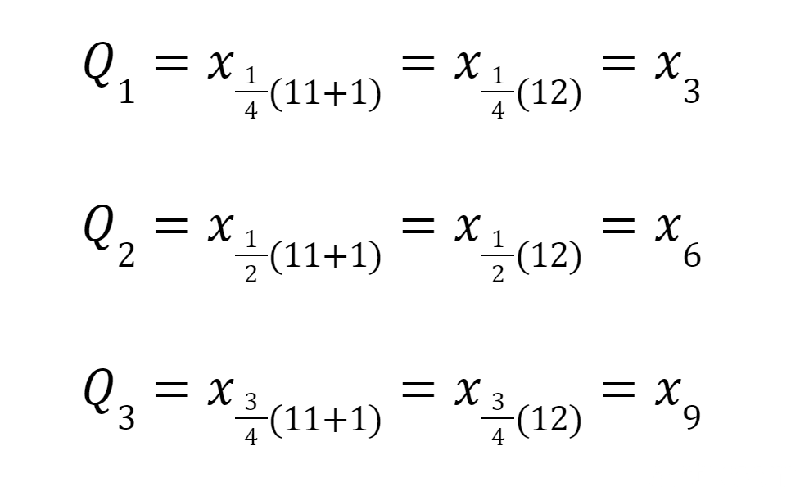 Contoh Soal. Foto: Bayu Ardi Isnanto/detikcom Contoh Soal. Foto: Bayu Ardi Isnanto/detikcom |
Maka Q1 adalah x ke-3, yaitu 5
Maka Q2 adalah x ke-6, yaitu 8
Maka Q3 adalah x ke-9, yaitu 10
Contoh 2
Berikut ini data berkelompok mengenai berat badan siswa di kelas VII. Carilah Q1-nya!
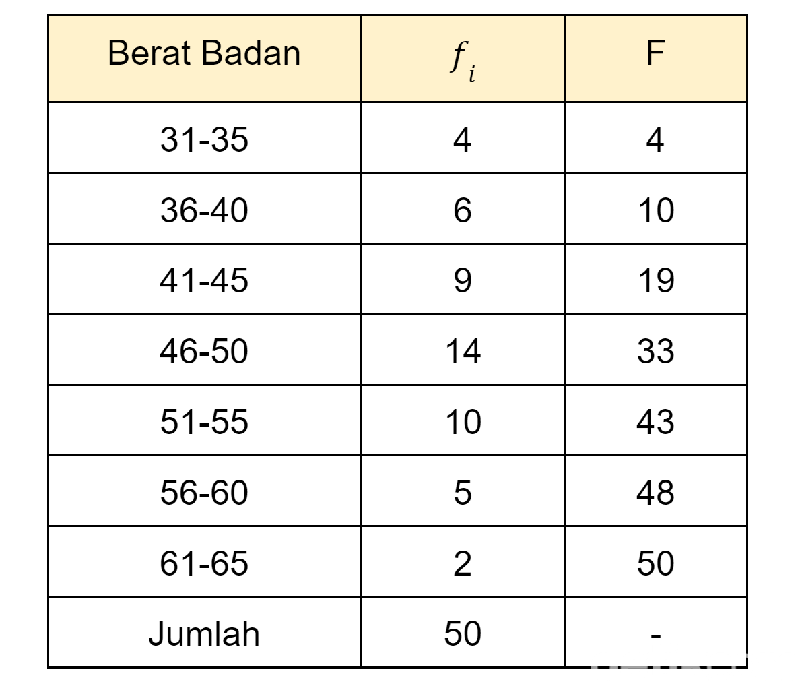 Tabel Berat Badan Siswa di Kelas VII. Foto: Bayu Ardi Isnanto/detikcom Tabel Berat Badan Siswa di Kelas VII. Foto: Bayu Ardi Isnanto/detikcom |
Untuk mencari Q1, maka kita cari kuartil 1 berada di interval mana. Cara dengan membagi jumlah frekuensi dengan 4. Maka 50/4 = 12,5. Jadi letak Q1 berada di interval 41-45.
Dengan demikian, diketahui bahwa:
L1 = 41-0,5 = 40,5
F1 = frekuensi kumulatif pada interval sebelumnya, yaitu 10
f1 = 9
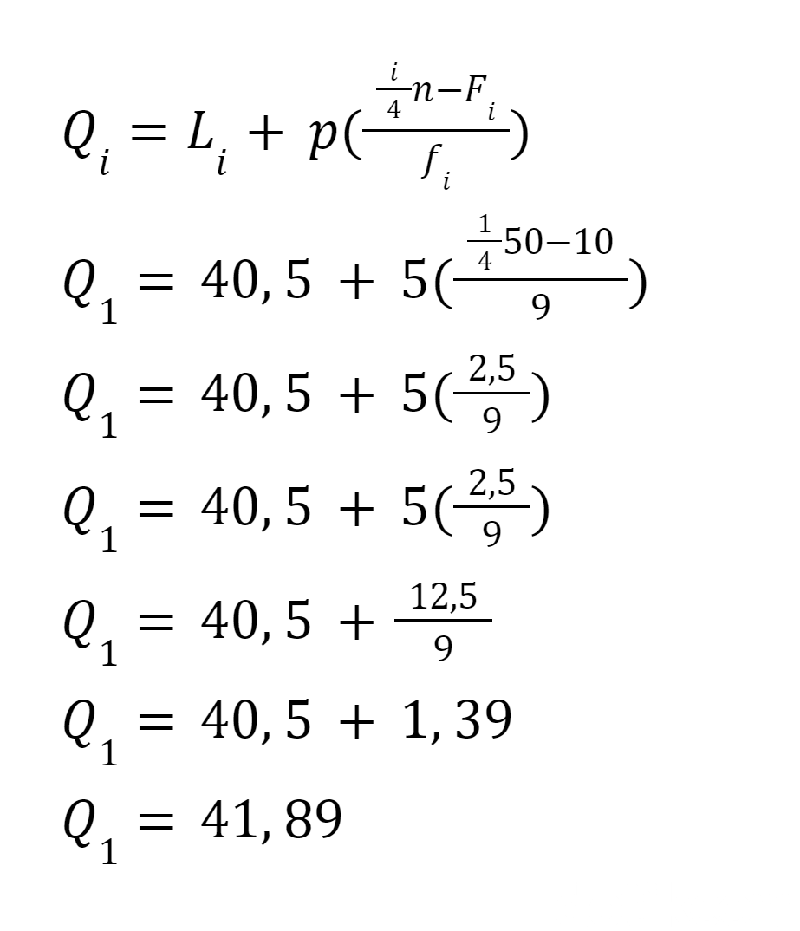 Contoh Soal. Foto: Bayu Ardi Isnanto/detikcom Contoh Soal. Foto: Bayu Ardi Isnanto/detikcom |
Itulah tadi telah kita ketahui rumus kuartil untuk data tunggal, baik ganjil maupun genap, serta data berkelompok, lengkap dengan contohnya. Semoga bermanfaat.
(bai/inf)


























































