.webp)
Statistika umumnya diajarkan sebagai topik mata pelajaran matematika pada tingkat Sekolah Menengah Atas (SMA) pada kelas 12. Materi ini akan memberikan pemahaman dasar mengumpulkan, mengorganisir, dan menganalisis data.
Statistika mencakup konsep dasar seperti mean, median, modus, kuartil, desil, persentil, rentang, hamparan, simpangan, hingga varians. Setiap konsep memiliki rumus statistika tersendiri yang perlu diingat untuk mencari jawabannya.
Berikut adalah rumus-rumus statistika pada pelajaran matematika
SCROLL TO CONTINUE WITH CONTENT
Rumus-Rumus Statistika
Dilansir dari beberapa sumber, berikut ini adalah kumpulan rumus statistika matematika.
Mean (Rata-rata)
Mean adalah nilai rata-rata dari keseluruhan data dibagi dengan banyaknya data. Bentuk rumus mencari mean dari data tunggal:
 Rumus mean data tunggal. Foto: Fida Afra/detikcom |
Keterangan:
X = mean
n = jumlah
Xi = nilai x ke i hingga n
∑ = epsilon (Jumlah)
Untuk menghitung mean dari data kelompok, terdapat rumus yang sedikit berbeda. Bentuk rumus untuk mencari mean dari data kelompok:
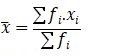 Rumus mean data kelompok. Foto: Fida Afra/detikcom |
Keterangan:
X = mean
xi = nilai tengah kelompok data ke-i
fi = frekuensi kelompok data ke-i
Median
Median adalah nilai tengah dalam sebuah himpunan data yang telah diurutkan. Berikut rumus untuk mencari nilai tengah dalam himpunan data:
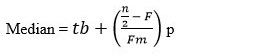 Rumus median. Foto: Fida Afra/detikcom |
Keterangan:
Tb = Tepi bawah dari kelas n/2
F = Frekuensi kumulatif sebelum kelas median
Fm = Frekuensi kelas median
p = Interval
Modus
Modus merupakan data dengan jumlah atau frekuensi sering muncul atau paling tinggi. Berikut adalah rumus untuk mencari modus dalam himpunan data:
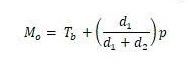 Rumus modus. Foto: Fida Afra/detikcom |
Keterangan:
Mo = Modus
Tb = Batas bawah kelas modus data kelompok
d1 = selisih frekuensi kelas modus dengan sebelum kelas modus
d2 = selisih frekuensi kelas modus dengan setelah kelas modus
p = panjang kelas interval
Kuartil
Kuartil adalah nilai-nilai yang membagi data setelah diurutkan dari data terkecil sampai data terbesar menjadi empat bagian sama besar. Berikut adalah rumus untuk mencari kuartil pada data tunggal:
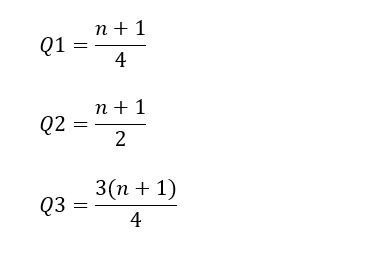 Rumus kuartil data tunggal. Foto: Fida Afra/detikcom |
Keterangan:
Q1 = Kuartil bawah
Q2 = Kuartil tengah
Q3 = Kuartil atas
Untuk menghitung kuartil pada data kelompok terdapat rumus yang berbeda, yaitu:
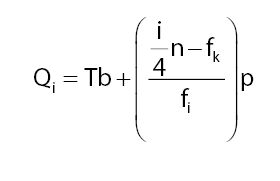 Rumus kuartil data kelompok. Foto: Fida Afra/detikcom |
Keterangan:
Q = Kuartil
i = 1,2,3
p = Panjang kelas interval
Tb = Tepi bawah kelas kuartil
fk= jumlah frekuensi sebelum kelas kuartil
fi = frekuensi kelas kuartil
n = jumlah seluruh frekuensi
Desil
Desil adalah istilah dalam statistika untuk membagi kelompok data menjadi sepuluh bagian sama rata. Berikut adalah rumus menghitung desil:
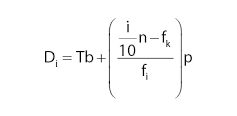 Rumus desil. Foto: Fida Afra/detikcom |
Keterangan:
D = Desil
i = Bilangan bulat kurang dari 10
n = jumlah frekuensi sebelum kelas desil
fk = jumlah frekuensi sebelum kelas desil
fi = frekuensi kelas desil
p = panjang kelas interval
Persentil
Persentil adalah metode statistika untuk membagi data menjadi 100 bagian sama besar. Berikut adalah rumus untuk menghitung persentil:
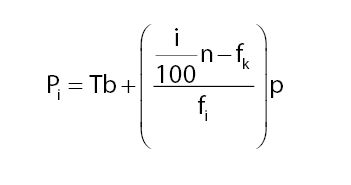 Rumus persentil data kelompok. Foto: Fida Afra/detikcom |
Keterangan:
P= Persentil
i = bilangan bulat kurang dari 100
Tb = tepi bawah kelas persentil
n = jumlah seluruh frekuensi
fk = jumlah frekuensi sebelum kelas persentil
fi = frekuensi kelas persentil
p = panjang kelas interval
Rentang (Jangkauan)
Rentang atau disebut juga jangkauan adalah selisih antara data nilai terbesar dengan nilai terkecil. Berikut ini adalah rumus menghitung rentang:
R = Xt - Xr
Keterangan:
R = Rentang
Xt = data terbesar dalam kelompok
Xr = data terkecil dalam kelompok
Hamparan
Hamparan adalah selisih antara kuartil ketiga (Q3) dengan kuartil pertama (Q1). Berikut ini adalah rumus untuk menghitung hamparan:
H = Q3 - Q1
Keterangan:
H = Hamparan
Q3 = Kuartil ketiga
Q1 = Kuartil pertama
Simpangan Kuartil
Simpangan kuartil adalah setengah dari hamparan atau jangkauan antar kuartil atau hasil kali selisih ketiga dengan kuartil pertama. Berikut ini adalah rumus untuk menghitung simpangan kuartil:
Qd = 1/2 (Q3 - Q1)
Keterangan:
Qd = Simpangan kuartil
Q3 = Kuartil ketiga
Q1 = Kuartil pertama
Simpangan Rata-rata
Simpangan rata-rata adalah rata-rata jarak antara nilai-nilai data menuju rata-ratanya. Berikut ini adalah rumus untuk menghitung simpangan rata-rata:
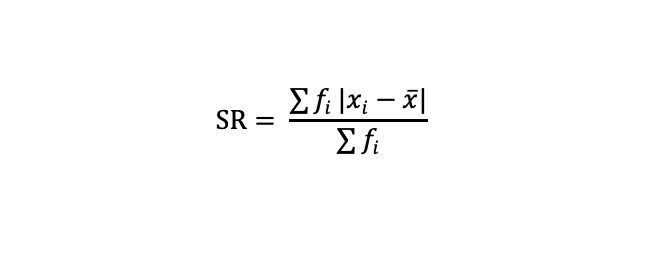 Simpangan rata-rata. Foto: Fida Afra/detikcom |
Keterangan:
SR = simpangan rata-rata
xi = nilai data ke-i
x = nilai rata-rata data
fi = total frekuensi data
|X - Xi| = Harga mutlak dari Xi - X yang selalu menghasilkan nilai positif.
∑ = Jumlah seluruh data dari i = 1 sampai i = n
Varians (Ragam)
Varians atau ragam adalah parameter kuadrat jarak suatu data terhadap rata-ratanya
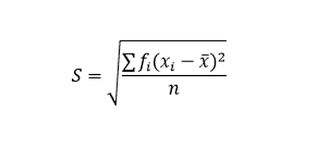 Rumus varians. Foto: Fida Afra/detikcom |
Keterangan:
S2= Varians
f = frekuensi
xi = nilai data ke-i
x = nilai rata-rata hitung
n = jumlah data dalam sampel
∑ = lambang penjumlahan
Itulah penjelasan mengenai pengertian dan cara menghitung rumus statistika yang tepat. Semoga dapat membantu ya, detikers!
(inf/inf)
