Perpangkatan dan Bentuk Akar: Sifat-sifat dan Contoh Soalnya

Dalam matematika, kita mengenal perpangkatan dan bentuk akar. Pangkat merupakan bentuk perkalian berulang pada angka yang sama. Sedangkan akar adalah kebalikannya, yaitu berupa pembagian berulang.

Untuk mengetahui penjelasan lebih lengkap, simak artikel di bawah ini, lengkap dengan sifat-sifat perpangkatan dan bentuk akar, beserta contoh soal dan jawabannya.

Sifat-sifat Bilangan Berpangkat

Untuk mengenal apa itu bilangan berpangkat, kita perlu mengetahui sifat-sifatnya terlebih dahulu.

Berikut ini sifat-sifat bilangan berpangkat dan bentuk akar yang dikutip dari buku Perpangkatan dan Bentuk Akar: Soal dan Pembahasan (2021) oleh Eva Risdaniati, dkk.

Sifat-sifat dari bilangan berpangkat adalah sebagai berikut:

1. Perkalian Berulang

Sifat paling umum dan mendasar adalah bahwa bilangan berpangkat sama dengan perkalian berulang. Misalnya sebagai berikut:

5¹ dibaca lima pangkat satu = 5
5² dibaca lima pangkat dua = 5 x 5
5⁴ dibaca lima pangkat empat = 5 x 5 x 5 x 5

2. Perkalian dan Pembagian Bilangan Berpangkat dengan Bilangan Pokok Sama

Perkalian bilangan bulat berpangkat dengan bilangan pokok yang sama, maka dapat diubah menjadi bentuk seperti ini:

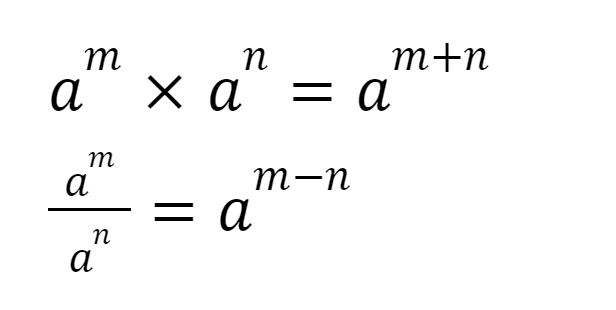Perkalian dan Pembagian Bilangan Berpangkat dengan Bilangan Pokok Sama.

Contoh 1:

2² x 2³ = 2²⁺³
4 x 8 = 2⁵
= 32

Contoh 2:

3⁵ ÷ 3³ = 3^5-3
243 ÷ 27 = 3²
= 9

3. Perkalian dan Pembagian Bilangan Berpangkat dengan Pangkat Sama

Perkalian dan pembagian bilangan berpangkat dengan pangkat yang sama bisa ditulis seperti ini:

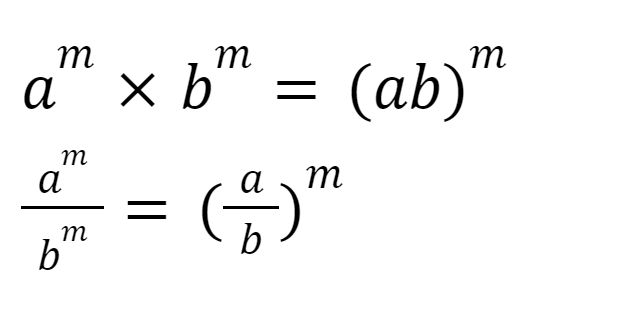Perkalian dan Pembagian Bilangan Berpangkat dengan Pangkat Sama.

Contoh 1:

5² x 7² = (5x7)²
25 x 49 = 35²
= 1.225

Contoh 2:

10²/5² = (10/5)²
100/25 = 2²
= 4

4. Pangkat Bilangan Berpangkat

Lantas bagaimana bilangan berpangkat diberi pangkat lagi?

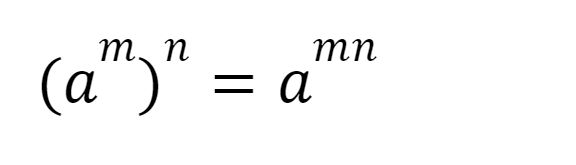Pangkat Bilangan Berpangkat.

Contohnya:

(4²)³ = 4^2.3
16³ = 4⁶
= 4.096

5. Bilangan Berpangkat Nol

Berapa pun bilangan yang diberi pangkat nol, hasilnya adalah 1.

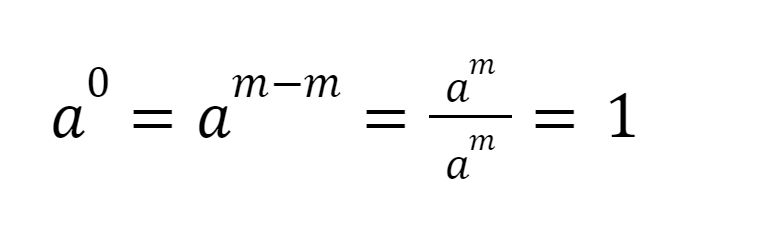Bilangan Berpangkat Nol. Foto: Perpangkatan dan Bentuk Akar: Soal dan Pembahasan (2021) oleh Eva Risdaniati, dkk

6. Penjumlahan dan Pengurangan Bilangan Berpangkat

Penjumlahan bilangan berpangkat dapat dibuat sederhana seperti contoh berikut ini:

3¹¹ + 3¹² = (3 × 3¹¹) + 3¹¹
= (3 + 1) × 3¹¹
= 4 × 3¹¹

Pengurangan bilangan berpangkat dapat dibuat sederhana seperti contoh berikut ini:

32^𝑛 − 2¹³ − (2^5𝑛 − 2¹⁵)
= (2⁵) − 2¹³ − 2^5𝑛 + 2¹⁵
= 2^5𝑛 − 2^5𝑛 + 2¹⁵ − 2¹³
= 2¹⁵ − 2¹³
= (2² × 2¹³) − 2¹³
= (4 × 2¹³) − 2¹³
= (4 − 1)2¹³
= 3 × 2¹³

7. Bilangan Berpangkat Negatif

Bilangan berpangkat negatif bisa diubah menjadi pangkat positif, namun bilangan pokoknya harus dibalik menjadi pecahan, seperti berikut ini:

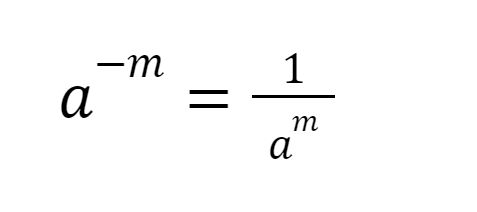Bilangan Berpangkat Negatif.

Contohnya:

10^-1 = 1/10
10^-2 = 1/10² = 1/100
10^-5 = 1/10⁵ = 1/100.000

Sifat Bentuk Akar

Masih mengutip dari buku Perpangkatan dan Bentuk Akar: Soal dan Pembahasan (2021) oleh Eva Risdaniati, dkk.

Sifat-sifat dari bentuk akar adalah sebagai berikut:

1. Kebalikan dari Bilangan Berpangkat

Bentuk akar (√) adalah kebalikan dari bilangan berpangkat. Jika 5² = 25, maka √25 = 5. Jika 2³ = 8, maka ³√8 = 2.

2. Bentuk Lain dari Akar

Bentuk akar bisa ditulis dengan bentuk pangkat seperti contoh berikut ini:

√25 = 25^1/2
3√216 = 216^1/3 = (6³)^1/3 = 6¹ = 6

3. Perkalian dan Pembagian Bentuk Akar

Berikut ini sifat-sifat yang perlu kamu ketahui:

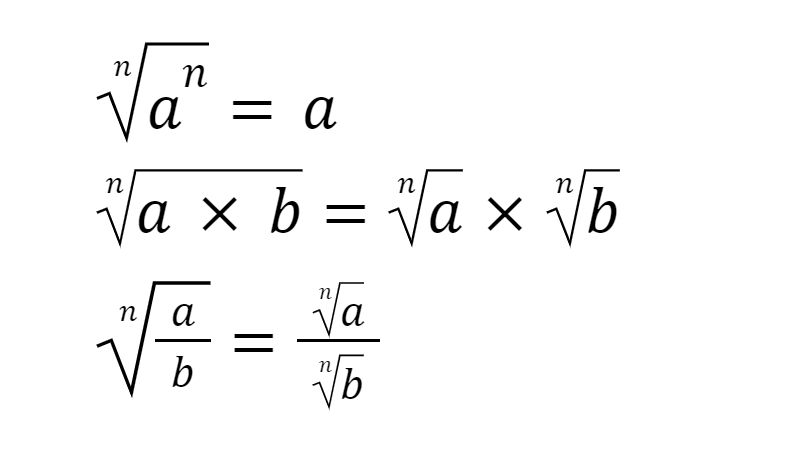Perkalian dan Pembagian Bentuk Akar.

Contoh 1:

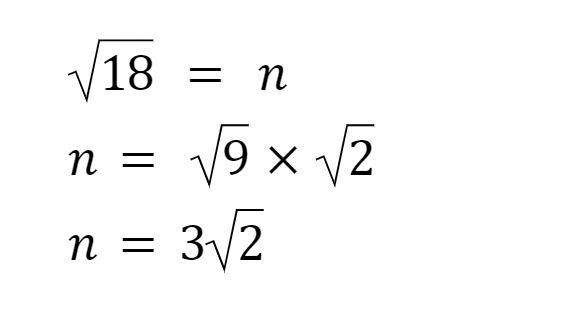Perkalian dan Pembagian Bentuk Akar.

Contoh 2:

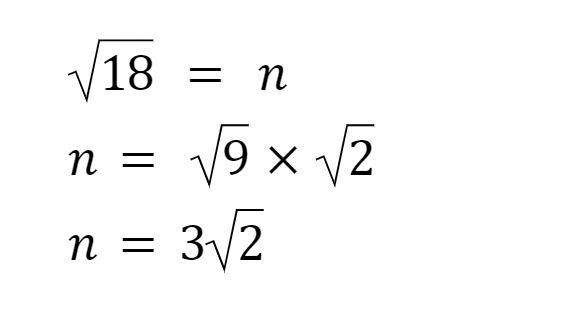Perkalian dan Pembagian Bentuk Akar.

Contoh 3:

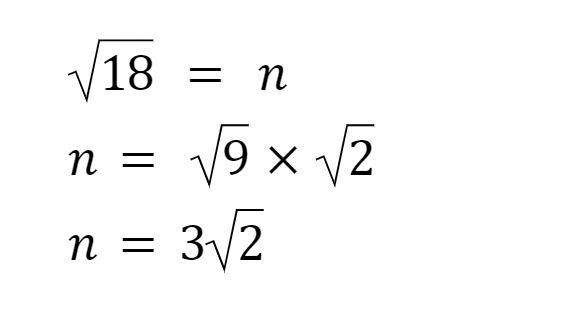Perkalian dan Pembagian Bentuk Akar.

4. Penjumlahan dan Pengurangan Bentuk Akar

Penjumlahan dan pengurangan bentuk akar mirip dengan penjumlahan dan pengurangan pada aljabar.

Misalnya 3^p + 5^p = (3 + 5)^p = 8^p. Sedangkan pada 3^p + 5^x, ini tidak dapat disederhanakan karena memiliki variabel berbeda.

Jika diterapkan pada bentuk akar, maka akan menjadi seperti ini:

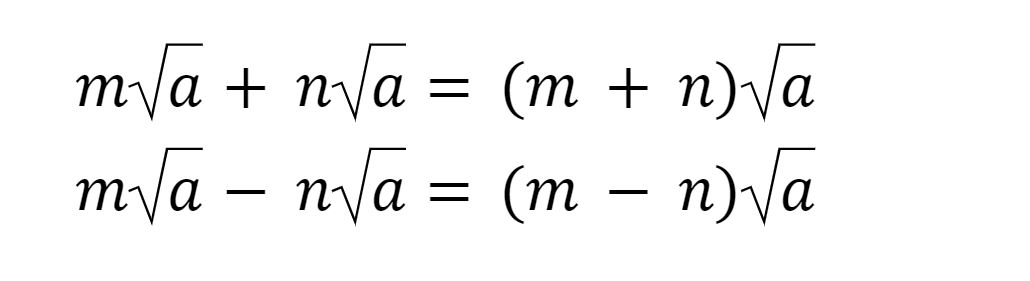Penjumlahan dan Pengurangan Bentuk Akar.

Contoh 1:

³√7 + ²√7
= ⁽³⁺²⁾√7
= ⁵√7

Contoh 2:

⁹√5 - ¹⁰√5
= ^(9-10)√5
= ^-√5

Demikian tadi materi matematika tentang perpangkatan dan bentuk akar, lengkap dengan sifat-sifat, contoh soal, dan jawabannya.

Video Trump Sebut Mahasiswa Tak Bisa Hitung 2+2 tapi Malah ke Harvard

Video Trump Sebut Mahasiswa Tak Bisa Hitung 2+2 tapi Malah ke Harvard