- Perbandingan Trigonometri Suatu Sudut Pada Segitiga siku-Siku
- Contoh Soal Perbandingan Trigonometri Pada Segitiga Siku-siku
- Perbandingan Trigonometri Sudut-sudut Istimewa 1. Nilai Perbandingan Trigonometri untuk Sudut 00 2. Nilai Perbandingan Trigonometri untuk Sudut 300 3. Nilai Perbandingan Trigonometri untuk Sudut 450 4. Nilai Perbandingan Trigonometri untuk Sudut 600 5. Nilai Perbandingan Trigonometri untuk Sudut 900
- Rangkuman Nilai Perbandingan Trigonometri Sudut Istimewa
- Contoh Soal Perbandingan Trigonometri Sudut Istimewa
Trigonometri adalah salah satu materi dari cabang ilmu matematika yang banyak kegunaannya. Umumnya, materi ini diajarkan sejak kelas 10 bangku Sekolah Menengah Atas.
Dalam kehidupan nyata, trigonometri dapat digunakan untuk memecahkan berbagai masalah. Mulai dari menghitung tinggi bangunan/gunung/pohon/bukit/benda, navigasi, menghitung ketinggian gelombang laut, astronomi, teknik sipil, dan arsitektur.
Dirangkum dari Modul Pembelajaran SMA Matematika Umum Kelas X yang diterbitkan oleh Kemdikbud, berikut penjelasan mengenai rumus trigonometri dan contoh soal serta penyelesaiannya.
SCROLL TO CONTINUE WITH CONTENT
Perbandingan Trigonometri Suatu Sudut Pada Segitiga siku-Siku
Jika ada sebuah segitiga ABC dengan titik sudut siku-siku di C. Panjang sisi di depan sudut A adalah a satuan, panjang sisi di depan sudut B adalah B satuan, dan panjang sisi di depan sudut C adalah c satuan.
Berikut adalah perbandingan trigonometri pada segitiga siku-siku.
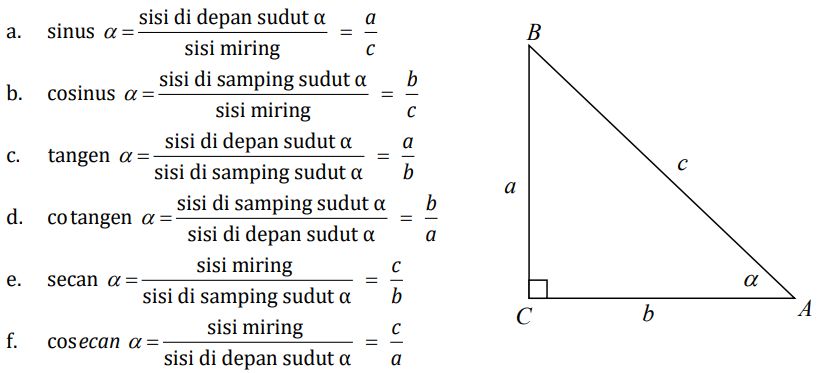 Foto: dok. Kemendikbudristek Foto: dok. Kemendikbudristek |
Keterangan:
- Sinus: sin
- Cosinus: cos
- Tangen: tan
- Cotangen: cot
- Secan: sec
- Cosecan: cosec atau csc.
Berdasarkan perbandingan yang telah dibuat, maka rumus-rumus dasar trigonometri adalah sebagai berikut.
 Foto: dok. Kemendikbudristek Foto: dok. Kemendikbudristek |
Contoh Soal Perbandingan Trigonometri Pada Segitiga Siku-siku
Berikut adalah contoh soal dan penyelesaian untuk perbandingan trigonometri pada segitiga siku-siku.
1. Diketahui segitiga ABC siku-siku di C dengan panjang sisi ∝ = √5 satuan dan panjang sisi b = 2 satuan. Jika Penyelesaian: Nilai c dihitung dengan menggunakan Pythagoras. Jadi, nilai perbandingan trigonometri untuk sudut ∝ adalah: 2. Diketahui cos ∝0 = 1/2 dan ∝0 sudut lancip (00 < ∝0 < 900). Carilah nilai perbandingan sudut ∝0 yang lain. Penyelesaian: Nilai a dicari dengan menggunakan Pythagoras. Jadi, nilai perbandingan ∝ yang lain adalah: Sudut istimewa artinya sebuah sudut dengan nilai perbandingan trigonometri yang dapat ditentukan secara langsung, tanpa harus menggunakan daftar trigonometri maupun kalkulator. Sudut-sudut tersebut antara lain 00, 300, 450, 600, dan 900. Berdasarkan penjelasan di atas, maka diperoleh hubungan trigonometri sebagai berikut. Agar lebih mudah diingat, berikut adalah tabel yang berisi nilai perbandingan trigonometri sudut istimewa. Berikut adalah contoh soal dan penyelesaian perbandingan trigonometri sudut istimewa. 1. Hitunglah: Penyelesaian: 2. Tunjukkan bahwa: Penyelesaian: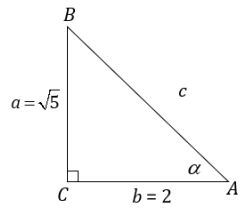 Foto: dok. Kemendikbudristek
Foto: dok. Kemendikbudristek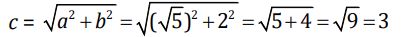 Foto: dok. Kemendikbudristek
Foto: dok. Kemendikbudristek
 Foto: dok. Kemendikbudristek
Foto: dok. Kemendikbudristek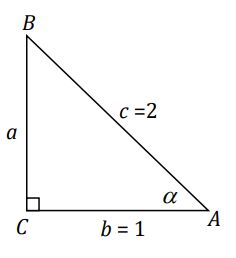 Foto: dok. Kemendikbudristek
Foto: dok. Kemendikbudristek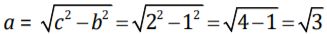 Foto: dok. Kemendikbudristek
Foto: dok. Kemendikbudristek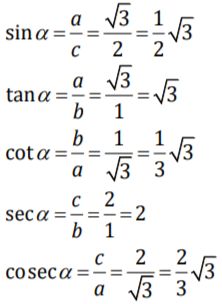 Foto: dok. Kemendikbudristek
Foto: dok. KemendikbudristekPerbandingan Trigonometri Sudut-sudut Istimewa
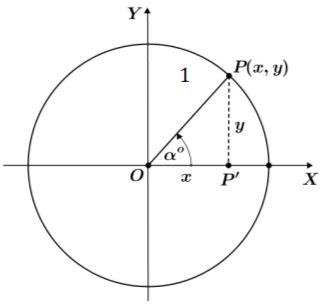
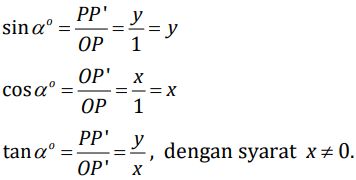
 Foto: dok. Kemendikbudristek.
Foto: dok. Kemendikbudristek.1. Nilai Perbandingan Trigonometri untuk Sudut 00
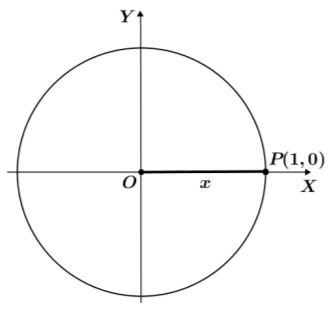
 Foto: dok. Kemendikbudristek
Foto: dok. Kemendikbudristek2. Nilai Perbandingan Trigonometri untuk Sudut 300
 Foto: dok. Kemendikbudristek
Foto: dok. Kemendikbudristek3. Nilai Perbandingan Trigonometri untuk Sudut 450

 Foto: dok. Kemendikbudristek
Foto: dok. Kemendikbudristek4. Nilai Perbandingan Trigonometri untuk Sudut 600
 Foto: dok. Kemendikbudristek
Foto: dok. Kemendikbudristek5. Nilai Perbandingan Trigonometri untuk Sudut 900
 Foto: dok. Kemendikbudristek
Foto: dok. KemendikbudristekRangkuman Nilai Perbandingan Trigonometri Sudut Istimewa
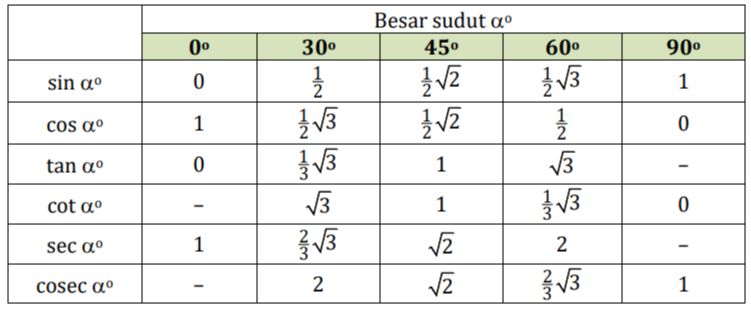 Foto: dok. Kemendikbudristek
Foto: dok. KemendikbudristekContoh Soal Perbandingan Trigonometri Sudut Istimewa
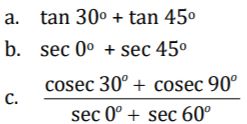 Foto: dok. Kemendikbudristek
Foto: dok. Kemendikbudristek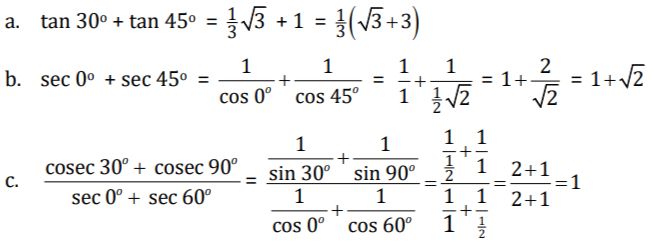 Foto: dok. Kemendikbudristek
Foto: dok. Kemendikbudristek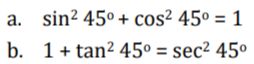 Foto: dok. Kemendikbudristek
Foto: dok. Kemendikbudristek Foto: dok. Kemendikbudristek
Foto: dok. Kemendikbudristek
(fds/fds)


























































