Rumus standar deviasi dikenal dalam ilmu statistik. Rumus ini bisa digunakan untuk mengetahui seberapa besar penyimpangan data yang menyebar dari titik pusatnya.
Sebelum mengetahui rumusnya, ada baiknya agar detikers terlebih dahulu mengenal apa itu standar deviasi. Simak uraian di bawah ini, ya.
Apa Itu Standar Deviasi?
Menukil buku Pengantar Statistika oleh Romansyah Sahabuddin, dkk, standar deviasi diketahui termasuk salah satu ukuran penyebaran data atau dispersi. Parameter ini menunjukkan rata-rata penyimpangan data dari nilai rata-ratanya (mean).
SCROLL TO CONTINUE WITH CONTENT
Standar deviasi atau disebut juga simpangan baku, merupakan ukuran penyebaran data dalam statistika yang penting dan paling banyak digunakan. Lantaran semua rangkaian data dipertimbangkan sehingga lebih stabil daripada parameter lainnya.
Istilah standar deviasi sendiri pertama kali diungkap oleh Karl Pearson pada tahun 1894. Yang mana ia menyebutkannya dalam buku berjudul On The Dissection of Asymmetrical Frequency Curves.
Simpangan baku merupakan akar kuadrat dari varians, yakni ukuran jarak sejumlah nilai data dari mean mereka. Jika varians ditarik akarnya maka akan menghasilkan standar deviasi. Oleh sebab itu, standar deviasi bisa dikatakan sebagai akar dari varians.
Kegunaan Standar Deviasi
Dikutip dari buku Statistika Deskriptif oleh Tri Andjarwati, dkk, standar deviasi sebagai ukuran penyebaran terbaik dan absolut digunakan untuk membandingkan suatu rangkaian data dengan rangkaian data lainnya.
Standar deviasi dapat pula digunakan untuk mengetahui apakah data yang seorang peneliti miliki tergolong baik atau tidak. Dibilang baik jika simpangan baku atau deviasi standarnya kecil. Dengan begitu dipahami bahwa data tersebut tidak terlalu tersebar atau tidak terlalu menyimpang dari pusat data.
Tak hanya itu, simpangan baku juga mampu memberitahu peneliti seberapa jauh data dari nilai rata-ratanya (mean).
Rumus Standar Deviasi
Berikut rumus standar deviasi data tunggal populasi maupun sampel sebagaimana dikutip dari laman kemdikbud.go.id:
1. Rumus Standar Deviasi Data Populasi
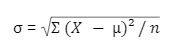 Foto: Azkia Nurfajrina/detikcom Foto: Azkia Nurfajrina/detikcom |
 Foto: Azkia Nurfajrina/detikcom Foto: Azkia Nurfajrina/detikcom |
2. Rumus Standar Deviasi Data Sampel
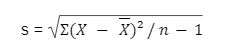 Foto: Azkia Nurfajrina/detikcom Foto: Azkia Nurfajrina/detikcom |
 Foto: Azkia Nurfajrina/detikcom Foto: Azkia Nurfajrina/detikcom |
Contoh Soal Standar Deviasi
Untuk bisa memahami rumus standar deviasi, mari perhatikan contoh soal standar deviasi data sampel:
Diberikan sampel dengan data: 8, 7, 10, 11, 4
Tentukan simpangan bakunya!
Penyelesaian:
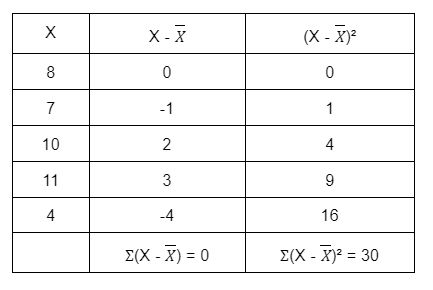 Foto: Azkia Nurfajrina/detikcom Foto: Azkia Nurfajrina/detikcom |
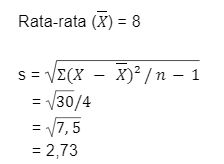 Foto: Azkia Nurfajrina/detikcom Foto: Azkia Nurfajrina/detikcom |
Jadi, standar deviasi susunan data tersebut adalah 2,73.
Itulah rumus standar deviasi tunggal populasi dan sampel beserta contoh soal dan jawabannya. Semoga bermanfaat!
(fds/fds)


























































