.webp)
Rumus ABC adalah rumus yang digunakan dalam mencari akar-akar dari suatu persamaan kuadrat di matematika.
Apabila dalam menyelesaikan persamaan kuadrat menggunakan pemfaktoran lebih sulit, biasanya rumus ABC yang akan digunakan. Rumus ABC seperti apa? Simak penjelasannya di bawah ini.
Penemu Rumus ABC
Dikutip dari e-book Rangkuman Matematika oleh Al Jupri dan Rohma Mauhibah, disebutkan bahwa penemu rumus ABC adalah Muhammad Ibnu Musa Al-Khawarizmi yang juga dikenal sebagai Bapak Aljabar.
SCROLL TO CONTINUE WITH CONTENT
Rumus ini pertama kali muncul dalam buku karya Al-Khawarizmi yang terkenal yaitu kitab Al Mukhtasar fi Hisab Aljabar wal Muqabbala. Buku tersebut juga merupakan buku aljabar pertama yang dibuat oleh matematikawan.
Berkat banyak penemuanya itu, Al-Khawarizmi dikenal sebagai salah satu ilmuwan Muslim yang berjasa di bidang matematika.
Metode Rumus ABC
Rumus persamaan kuadrat menggunakan metode rumus kuadrat atau rumus ABC.
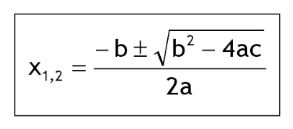 Bentuk rumus ABC. Foto: dok. Buku Rumus Jitu Matematika oleh Abdul Aziz dan Budhi Setyono. |
Mengapa disebut rumus ABC? Alasannya, karena a, b, dan c termasuk bilangan real, yang menjadi komponen di dalamnya.
Sementara x adalah variabel atau nilai yang belum diketahui dalam persamaan kuadrat. Di mana bisa berupa koefisien x², koefisien x, atau konstanta.
Rumus ABC menjadi rumus yang paling mudah untuk akar-akar di persamaan kuadrat.
Bentuk umum rumus ABC yaitu ax2 + bx + c = 0, atau bisa juga x₁ + x₂ = - b/a
Contoh Soal Rumus ABC dan Pembahasannya
Supaya detikers bisa lebih memahami metode rumus ABC, simak contoh soal rumus abc beserta hitunganya dalam persamaan kuadrat di bawah ini.
Soal 1
Hitunglah himpunan penyelesaian dari x2 - 2x - 4 = 0, menggunakan rumus ABC.
Jawab:
x2 - 2x - 4 = 0
a = 1, b = -2, c = -4
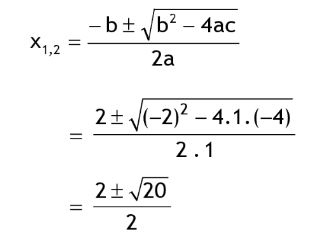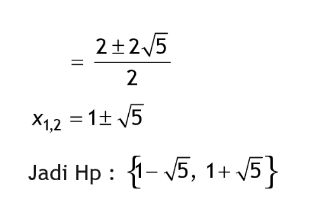 Contoh soal rumus ABC. Foto: dok. Buku Rumus Jitu Matematika oleh Abdul Aziz dan Budhi Setyono. |
 Contoh soal rumus ABC. Foto: dok. Buku Rumus Jitu Matematika oleh Abdul Aziz dan Budhi Setyono. |
Soal 2
Diketahui x₁ dan x₂ adalah akar-akar persamaan kuadrat 2x2 + 5x - 1 = 0. Hitunglah nilai dari 2x₁ + 2x₂ = ...
Jawab:
2x2 + 5x - 1 = 0
a = 1, b = 5, c = -1
Ingat bentuk rumus ABC: x₁ + x₂ = - b/a
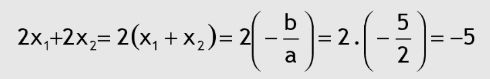 Contoh soal rumus ABC. Foto: Buku Rumus Jitu Matematika oleh Abdul Aziz dan Budhi Setyono. |
Nah, itu tadi penjelasan tentang rumus ABC yang ditemukan oleh Al-Khawarizmi, lengkap dengan contoh soal dan cara menghitungnya.
(khq/inf)
