Mengenal Rumus Turunan Matematika, Sifat, dan Contoh Soalnya

Ilustrasi matematika — Foto: Pixabay/geralt

Daftar Isi

Rumus dan Sifat-sifat Turunan
Rumus Turunan Fungsi Trigonometri
Contoh Soal Rumus Turunan

Jakarta -

Turunan merupakan pengukuran terhadap bagaimana fungsi dapat berubah seiring dengan perubahan nilai input. Secara umum, turunan dapat menunjukkan bagaimana suatu besaran dapat berubah akibat adanya perubahan besaran lainnya.

Materi rumus turunan dalam matematika umumnya diberikan di bangku sekolah menengah atas. Bagi kawan detikEdu yang ingin tahu lebih lanjut tentang rumus turunan, berikut pembahasannya.

Rumus dan Sifat-sifat Turunan

Dikutip dari E-Modul Matematika Kelas XI yang diterbitkan oleh Kemendikbud, berikut adalah rumus sifat-sifat turunan.

SCROLL TO CONTINUE WITH CONTENT

1. Turunan fungsi konstan: f(x) = k ⇒ f'(x) = 0

2. Turunan fungsi identitas : f(x) = x ⇒ f'(x) = 1.

3. Turunan fungsi aljabar berpangkat n

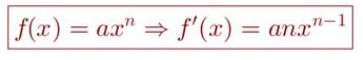Foto: dok. E-Modul Matematika Kelas XI Kemendikbud

4. Rumus turunan Jumlah dan selisih fungsi-fungsi

Foto: dok. E-Modul Matematika Kelas XI Kemendikbud

5. Turunan fungsi aljabar hasil kali

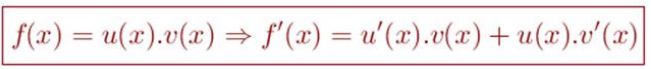Foto: dok. E-Modul Matematika Kelas XI Kemendikbud

6. Rumus turunan fungsi aljabar hasil kali diatas dapat diperluas untuk mencari rumus turunan yang terdiri dari tiga fungsi, yaitu:

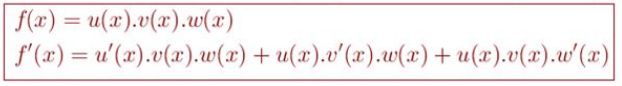Foto: dok. E-Modul Matematika Kelas XI Kemendikbud

7. Turunan fungsi aljabar hasil bagi, dengan syarat v(x) ≠ 0

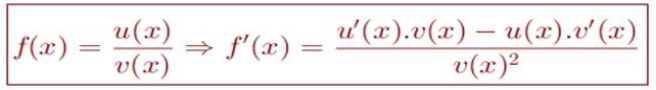Foto: dok. E-Modul Matematika Kelas XI Kemendikbud

8. Sifat-sifat turunan fungsi aljabar

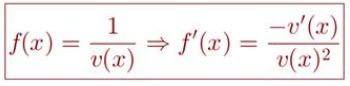Foto: dok. E-Modul Matematika Kelas XI Kemendikbud

Rumus Turunan Fungsi Trigonometri

Mengutip dari E-Modul Matematika Kelas XI yang diterbitkan oleh Kemendikbud, berikut adalah deretan rumus turunan fungsi trigonometri.

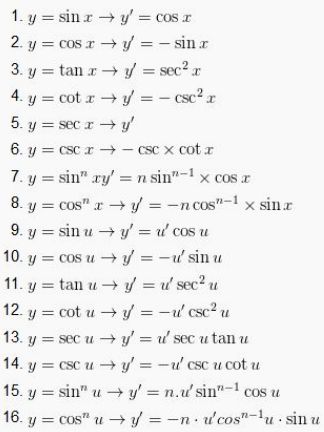Foto: dok. E-Modul Matematika Kelas XI Kemendikbud

Contoh Soal Rumus Turunan

Merujuk pada Modul Pembelajaran SMA Matematika Umum, berikut adalah contoh soal dan penyelesaian untuk rumus turunan.

1. Tentukan gradien garis singgung kurva y = x²+ 2x - 2 di titik (1, 1).

Penyelesaian:

a. Tentukan turunan pertama dari fungsi y

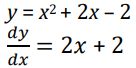Foto: dok. E-Modul Matematika Kelas XI Kemendikbud

b. Tentukan gradien garis singgung m

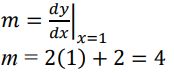Foto: dok. E-Modul Matematika Kelas XI Kemendikbud

c. Jadi, gradien garis singgung kurva adalah 2

2. Tentukan persamaan garis singgung dan garis normal pada kurva y = 2x3 - 5x2 - x + 6 di titik yang berabsis 1.

Penyelesaian:

a. Tentukan titik singgung (x_1,y₁)

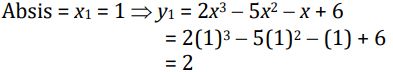Foto: dok. E-Modul Matematika Kelas XI Kemendikbud

Jadi, titik singgungnya adalah (1, 2).

b. Tentukan turunan pertama fungsi y

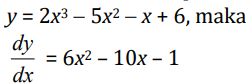dok. E-Modul Matematika Kelas XI Kemendikbud

c. Tentukan gradien m

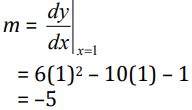Foto: dok. E-Modul Matematika Kelas XI Kemendikbud

d. Tentukan persamaan garis singgung

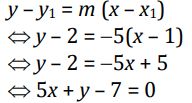Foto: dok. E-Modul Matematika Kelas XI Kemendikbud

e. Tentukan persamaan garis normal

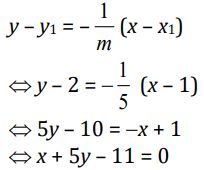Foto: dok. E-Modul Matematika Kelas XI Kemendikbud

f. Kesimpulan

Jadi, persamaan garis singgung kurva y = 2x³ - 5x² - x + 6 di titik yang berabsis 1 adalah 5x + y - 7 = 0 dan persamaan garis normalnya adalah x + 5y - 11 = 0.