.webp)
Dalam matematika, terdapat istilah mean, median, dan modus. Fungsinya adalah untuk menyajikan data dengan kategori tertentu. Umumnya, data berupa hasil penelitian atau observasi.
Kali ini, detikEdu akan fokus membahas mengenai median. Median (Me) atau kuartil sendiri merupakan nilai tengah dari kumpulan data. Tentunya, nilai tengah ini bisa diketahui setelah mengurutkan dari data terkecil hingga terbesar, dan sebaliknya.
Dirangkum dari berbagai sumber, berikut pembahasan lengkap mengenai rumus median.
SCROLL TO CONTINUE WITH CONTENT
Rumus Median Data Tunggal
Median data tunggal dapat dicari dengan cara berikut.
- Apabila banyak data adalah ganjil, maka mediannya terletak tepat di tengah setelah data diurutkan
- Apabila banyak data adalah genap, maka median adalah rata-rata dari dua data yang terletak di tengah setelah diurutkan.
Contoh Soal Rumus Median Tunggal
1. Tentukan Median dari data
a. 7, 8, 3, 4, 9, 10, 4
b, 5, 7, 3, 8, 5, 6, 10, 9
Penyelesaian:
a. Data diurutkan terlebih dahulu menjadi 3, 4, 4, 7, 8, 9, 10
Nilai yang berada di tengah adalah 7. Maka, median adalah 7.
b. Data diurutkan terlebih dahulu menjadi 3, 5, 5, 6, 7, 8, 9, 10
Nilai yang berada di tengah adalah 6 dan 7. Maka, median adalah
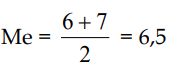 Foto: dok. LMS SPADA Kemdikbud |
Rumus Median Untuk Data Tidak Berkelompok
Dikutip dari LMS SPADA Kemdikbud, rumus median bisa digunakan untuk data tidak berkelompok yang disajikan secara tunggal maupun daftar frekuensi. Terdapat 3 langkah untuk rumus median ini, yakni:
- Mengurutkan data berdasarkan nilainya. Misalkan, data diurutkan dari data terkecil ke data terbesar.
- Menentukan letak median dengan rumus k = (n+1)/2 (n adalah banyak data)
- Menentukan nilai median dengan rumus berikut.
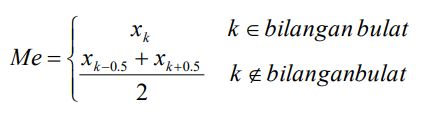 Foto: dok. LMS SPADA Kemdikbud |
Contoh Soal Rumus Median Untuk Data Tidak Berkelompok
1. Terdapat sampel dengan nilai-nilai data: 12, 34, 14, 34, 28, 34, 34, 28, 14. Tentukan median dari data tersebut!
Penyelesaian:
Data dapat diurutkan dari terkecil ke terbesar, atau dibuat dalam tabel distribusi frekuensi sebagai berikut:
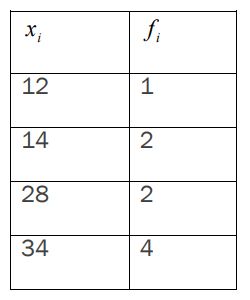 Foto: dok. LMS SPADA Kemdikbud |
Banyaknya data adalah 9. Jadi, median terletak pada data (9+1)/2, yakni pada data ke-5 yang nilainya 28. Kesimpulannya, median untuk data tersebut adalah 28.
Rumus Median Untuk Data Berkelompok
Berikutnya, ada juga rumus median untuk menghitung data berkelompok.
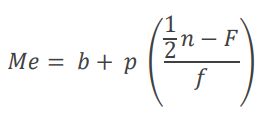 Foto: dok. LMS SPADA Kemdikbud |
Keterangan:
b = batas bawah kelas median, yakni kelas dimana median terletak
p = panjang kelas median
n = ukuran sampel/banyak data
F = jumlah semua frekuensi dengan tanda kelas lebih kecil dari tanda kelas median
f = frekuensi kelas median
Contoh Soal Rumus Median Untuk Data Berkelompok
1. Tentukan median dari nilai ujian 80 mahasiswa yang disajikan dalam daftar di bawah ini.
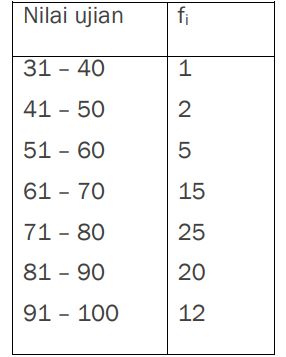 Foto: dok. LMS SPADA Kemdikbud |
Penyelesaian:
Setengah dari keseluruhan data (80) adalah 40. Jadi, median terletak pada kelas interval kelima, karena pada kelas tersebut ada data ke-40.
Median terletak pada interval 71-80 diperoleh nilai b = 70,5, f = 25, F = 1 + 2 + 5 + 15 = 23. Dengan formula tersebut, maka nilai median dari data tersebut adalah:
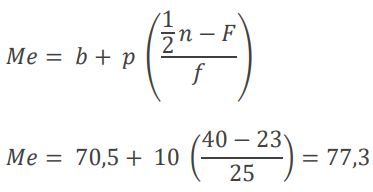 Foto: dok. LMS SPADA Kemdikbud |
(fds/fds)
