Dalam soal matematika bangun datar, terkadang ada soal tentang luas daerah yang diarsir. Biasanya, soal berupa bangun datar seperti persegi, persegi panjang atau lingkaran yang sebagian areanya diarsir.
Dalam satu bangunan, bisa ada dua bangun datar. Jadi, siswa diminta untuk menghitung luas pada daerah yang diarsir dalam bangun datar tersebut. Simak contoh soalnya berikut ini ya.
Luas daerah yang Diarsir Adalah
Luas daerah yang diarsir adalah selisih dari satu area dalam bangun datar dengan area lainnya. Selain itu, luas daerah yang diarsir juga bisa berkaitan dengan bilangan pecahan. Misalnya dalam gambar berikut ini:
SCROLL TO CONTINUE WITH CONTENT
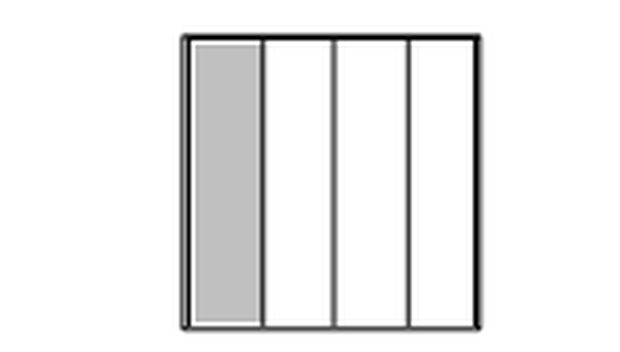 Luas daerah yang diarsir Foto: Andhin Dyas Fiolani/Modul Belajar Mandiri SIMPKB Luas daerah yang diarsir Foto: Andhin Dyas Fiolani/Modul Belajar Mandiri SIMPKB |
Luas daerah diarsir ini mewakili bilangan 1/4. Mengutip Modul Belajar Mandiri SIMPKB oleh Andhin Dyas Fiolani, M.Pd, bilangan pecahan ini merupakan perbandingan himpunan bagian yang sama dari suatu himpunan terhadap keseluruhan himpunan semula.
Contoh Soal Luas Daerah yang Diarsir
Soal yang akan dibahas berikut ini adalah mengenai luas daerah yang diarsir dalam sebuah bangun datar. Jadi, pastikan kamu sudah mengetahui rumus luas bangun datar ya. Berikut beberapa contoh soal mengutip Buku Kumpulan 100 Soal dan Pembahasan Bangun Datar oleh Abdul Muntolib dan Rizki Wahyu Yunian Putra, MPd:
1. Di bawah ini adalah gambar persegi ABCD dan persegi panjang FEHG! Jika luar daerah yang tidak diarsir adalah 68 cm2. Tentukan luas yang diarsir
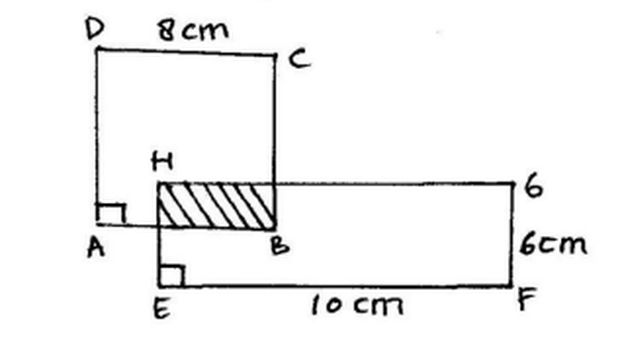 Luas daerah yang diarsir. Foto: Abdul Muntolib dan Rizki Wahyu Yunian Putra MPd/Buku Kumpulan 100 Soal dan Pembahasan Bangun Datar. Luas daerah yang diarsir. Foto: Abdul Muntolib dan Rizki Wahyu Yunian Putra MPd/Buku Kumpulan 100 Soal dan Pembahasan Bangun Datar. |
Jawab:
s (sisi)= 8 cm
p (panjang)=10 cm
l lebar)= 6 cm
Luas persegi= sxs = 8x8= 64 cm2
Luas persegi panjang= pxl= 10x6 =60 cm2
Misal luas yang diarsir=y, maka:
Luas yang tidak diarsir =(luas persegi-y)+(luas persegi panjang)-y)
68= (64-y)+(60-y)
68=124-2y
2y=124-2y
=56
=56/2
=28
Maka, luas daerah yang diarsir adalah 28 cm2
2. Suatu lingkaran tepat berada di dalam persegi seperti gambar. Jika panjang rusuk persegi adalah 14 cm, maka, berapakah luas daerah yang diarsir
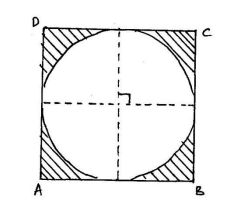 Luas daerah yang diarsir. Foto: Abdul Muntolib dan Rizki Wahyu Yunian Putra MPd/Buku Kumpulan 100 Soal dan Pembahasan Bangun Datar. Luas daerah yang diarsir. Foto: Abdul Muntolib dan Rizki Wahyu Yunian Putra MPd/Buku Kumpulan 100 Soal dan Pembahasan Bangun Datar. |
Jawab:
s (rusuk)=14 cm
r (jari-jari)=14/2 =7 cm
Luas arsir= luas persegi-luas lingkaran
= s2= πr2
= 14(kuadrat)-(22/7x7(kuadrat))
= 196=154
= 42cm2
Maka, luas daerah yang diarsir adalah 42 cm2.
3. Di bawah ini adalah gambar RSTU persegi dan KLMN persegi panjang. Jika luas bagian yang diarsir adalah 72 cm2, tentukan luas bagian yang tidak diarsir!
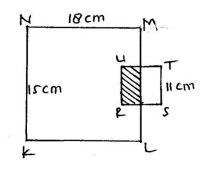 Luas daerah yang diarsir/Abdul Muntolib dan Rizki Wahyu Yunian Putra MPd/Buku Kumpulan 100 Soal dan Pembahasan Bangun Datar. Foto: Andhin Dyas Fiolani/Modul Belajar Mandiri SIMPKB Luas daerah yang diarsir/Abdul Muntolib dan Rizki Wahyu Yunian Putra MPd/Buku Kumpulan 100 Soal dan Pembahasan Bangun Datar. Foto: Andhin Dyas Fiolani/Modul Belajar Mandiri SIMPKB |
Jawab:
Luas KLMN= 18cm x15cm
= 270 cm2
Luas RSTU= 11x11
= 121 cm2
Misal luas yang diarsir adalah x, maka:
Luas daerah yang tidak diarsir
=(Luas KLMN-x)+(Luas RSTU-x)
=(270-72)+(121-72)
=247 cm2
4. Perhatikan gambar berikut! Jika B adalah titik pusat simetri putar persegi KLMN, maka, tentukan luas daerah yang diarsir.
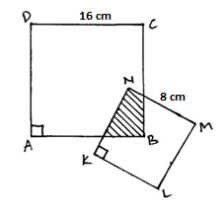 Luas daerah yang diarsir. Foto: Abdul Muntolib dan Rizki Wahyu Yunian Putra MPd/Buku Kumpulan 100 Soal dan Pembahasan Bangun Datar. Luas daerah yang diarsir. Foto: Abdul Muntolib dan Rizki Wahyu Yunian Putra MPd/Buku Kumpulan 100 Soal dan Pembahasan Bangun Datar. |
Jawab: Jika persegi KLMN diputar lurus sesuai dengan persegi ABCD pada titik pusat simetri B, maka daerah yang diarsir akan berbentuk persegi dengan panjang rusuk 1/2 dari rusuk persegi KLMN, yaitu 8/2= 4 cm. Jadi, luas daerah yang diarsir= 4x4= 16 cm2
5. ABCD merupakan persegi panjang dengan ukuran 10 cmx 6 cm. Jika FG adalah 6 cm, dan EF adalah 8 cm dan luas wilayah yang tidak diarsir adalah 58 cm2, maka tentukan luas daerah yang diarsir!
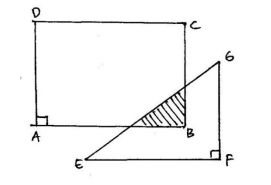 Luas daerah yang diarsir. Foto: Abdul Muntolib dan Rizki Wahyu Yunian Putra MPd/Buku Kumpulan 100 Soal dan Pembahasan Bangun Datar. Luas daerah yang diarsir. Foto: Abdul Muntolib dan Rizki Wahyu Yunian Putra MPd/Buku Kumpulan 100 Soal dan Pembahasan Bangun Datar. |
Jawab: Misal luas yang diarsir adalah Y
Luas daerah yang tidak diarsir=(luas persegi panjang-Y)
58= (10x6)+(8x6)/2-2Y
58= 60+24-2Y
58= 84-2Y
2Y= 84=58
2Y=26
Y = 13
Jadi, luas daerah yang diarsir adalah 13 cm
6. Tentukan luas daerah yang diarsir pada gambar di bawah ini
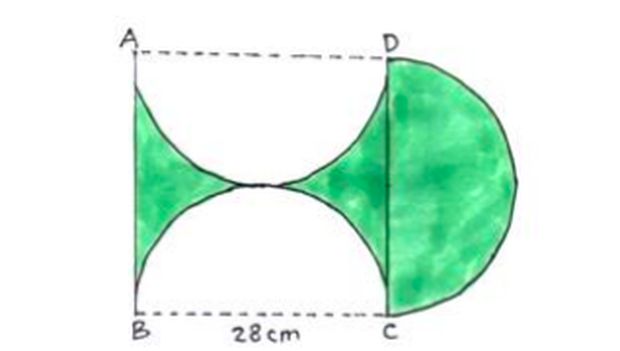 Luas daerah yang diarsir Foto: Andhin Dyas Fiolani/Modul Belajar Mandiri SIMPKB Luas daerah yang diarsir Foto: Andhin Dyas Fiolani/Modul Belajar Mandiri SIMPKB |
Jawab:
Luas daerah yang diarsir adalah
=luas persegi ABCD-luas lingkaran+ 1/2 luas lingkaran
=luas persegi ABCD-1/2 luas lingkaran
=(sisi2)-1/2 (πr2)
=(28x28)-1/2 (22/7x14x14)
=784-308
=476 cm2
Itulah informasi mengenai luas daerah yang diarsir beserta contoh soal dan penyelesaiannya. Semoga informasi ini membantumu.
(elk/row)


























































