Jaring-Jaring Balok: Pengertian, Rumus, Contoh Soal

Balok adalah salah satu jenis bangun ruang yang dipelajari dalam ilmu matematika. Di sekitar kita, ada banyak bangun ruang yang tersebar, contohnya kulkas, kotak pensil, lemari, dan lain sebagainya.

Seperti bangun ruang yang lain, balok tersusun atas potongan bangun datar. Potongan yang jika dirangkai sedemikian rupa bisa membentuk balok inilah yang disebut jaring-jaring.

Pengertian dan Contoh Jaring-jaring Balok

Jaring-jaring balok adalah bangun datar yang merupakan rangkaian tertentu dari dua bujur sangkar dan enam persegi panjang. Bila dilipat pada sisi-sisi yang tepat dapat membentuk balok.

Berikut contoh balok dan jaring-jaringnya dikutip dari buku Mari Memahami Konsep Matematika karya Wahyudin Djumanta

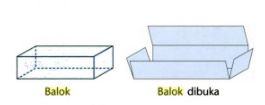jaring-jaring balok. Foto: Salsabila Azzahra/detikcom.

Sumber : Buku Matematika SD di Sekitar Kita untuk Sekolah Dasar kelas IV Semester 2

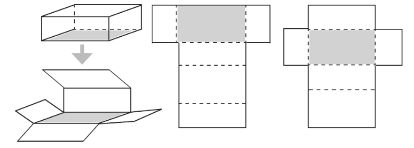jaring-jaring balok. Foto: Salsabila Azzahra/detikcom.

Sumber : Ensiklopedia Rumus Matematika SD kelas 4, 5, 6

Cara Membuat Jaring-jaring Balok

Sebuah balok memiliki 6 sisi, 12 rusuk, dan 8 simpul. Balok yang dibentuk oleh enam persegi yang kongruen disebut kubus. Jadi cara membuat jaring balok adalah sebagai berikut

1. Cetak pola pada karton

2. Kemudian potong karton mengikuti ruas garis yang terlihat

3. Buatlah lipatan-lipatan pada setiap jaring berdasarkan ruas-ruas garis hingga membentuk balok-balok yang hampir sempurna

4. Balok adalah hasil dari melipat dan merekatkan lidah jaring, dan dengan persegi panjang yang lebih rendah sebagai sisi depan

Karakteristik Balok

Membahas jaring-jaring balok tentu tidak lengkap jika tidak membahas bangunan balok sendiri. Berikut ciri-ciri sebua balok

1. Tulang rusuk

Tulang rusuk balok adalah garis perpotongan antara sisi-sisi balok. Ciri-ciri balok memiliki jumlah rusuk sebanyak 12 buah dengan panjang yang sama. Tulang rusuk ini terbagi menjadi 4 tulang rusuk dasar, 4 tulang rusuk tegak, dan 4 tulang rusuk atas. Tulang rusuk sejajar memiliki panjang yang sama

• 4 rusuk panjang = AB = DC = EF = HG
• 4 rusuk lebar = AD = BC = EH = FG
• 4 rusuk tinggi = AE = BF = CG = DH.

2. Ruang Diagonal

Ciri-ciri balok adalah ruang diagonal. Setiap ruang diagonal pada balok memiliki panjang yang sama. Diagonal ruang balok adalah ruas garis yang menghubungkan dua sudut balok yang berlawanan. Diagonal ruang balok berpotongan di tengah dan membagi dua diagonal ruang secara merata. Terdapat 4 diagonal ruang pada balok yang sama panjang

3. Memiliki 6 Sisi

Sisi balok menjadi batas antara balok dan tiga pasang sisi yang memiliki bentuk dan ukuran yang sama ketika saling berhadapan. Sebuah balok harus memiliki 6 sisi persegi atau persegi panjang. Sisi-sisi ini ada di kiri dan kanan, atas dan bawah, serta depan dan belakang

Berdasarkan contoh gambar balok di atas, maka 6 sisinya adalah:

• Sisi kiri dan sisi kanan = ADHE = BCGF
• Alas (bawah) dan atas = ABCD = EFGH
• Sisi depan dan sisi belakang = ABFE = DCGH.

4. Sisi Diagonal

Sisi/bidang diagonal suatu balok adalah ruas garis yang menghubungkan dua titik sudut yang berlawanan pada suatu sisi. Ada 12 sisi diagonal pada balok. Setiap bidang diagonal pada sisi yang berlawanan memiliki panjang yang sama

5. Bidang Diagonal

Diagonal balok adalah bidang yang melewati dua sisi yang berlawanan. Diagonal balok membagi balok menjadi dua bagian yang sama. Ada 6 bidang diagonal. Setiap bidang diagonal pada balok memiliki bentuk persegi panjang

Jika diperhatikan contoh gambar balok, maka 6 bidang diagonalnya adalah :

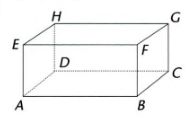balok Foto: Salsabila Azzahra/detikcom.

Sumber : Buku Matematika SD di Sekitar Kita untuk Sekolah Dasar kelas IV Semester 2

ACGE = bidang diagonal BDHF

ABGH = bidang diagonal DCFE

Bidang diagonal BCHE = ADGF.

6. Memiliki luas permukaan dan volume balok

Sebuah balok memiliki luas permukaan dan volume. Volume mengacu pada lebar ruangan di sebuah bangunan. Untuk menentukan luas dan volume suatu balok dapat diketahui dengan menggunakan rumus-rumus tertentu.

Rumus Luas Permukaan Balok

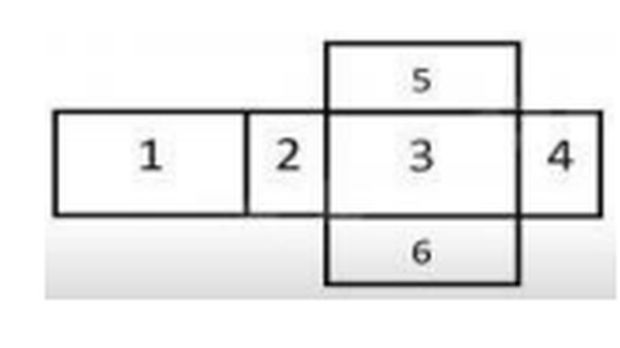jaring-jaring balok. Foto: Salsabila Azzahra/detikcom.

Sumber : Latihan Soal Matematika Materi Jaring-jaring Kubus dan Balok SD Muhammadiyah 4, Malang

Dari gambar di atas, kita mengetahui bahwa balok tersebut memiliki 3 pasang persegi panjang yang berukuran sama. Untuk menghitung luas permukaan, kita cukup menjumlahkan luas ketiga pasang persegi panjang tersebut. Ada 2 cara, yaitu:

Cara 1: Hitung luas tiga pasang sisi

L = pl + lt + pt + pl + lt + pt

L = 2pl + 2lt + 2pt

L = 2 (pl + lt + pt)

Metode 2: Menggunakan prinsip luas permukaan prisma

Yaitu menghitung luas alas, atap dan penutup. Karena luas alas = luas atap maka diperoleh rumusnya

L = 2 × Area dasar + Area Selimut

L = 2 × Luas alas + Lingkar alas × tinggi

L = 2 × pl + (p + l + p + l) × t

L = 2pl + (2p + 2l) × t

L = 2pl + 2lt + 2pt

L = 2 (pl + lt + pt)

Hasilnya sama. Jadi dapat disimpulkan bahwa rumus luas permukaan balok adalah L = 2 (pl + lt + pt) .

Contoh Soal Luas Permukaan Balok

Sebuah balok berukuran panjang 20 cm, lebar 14 cm, dan tinggi 10 cm. tentukan luas permukaan balok? Solusinya:

dikenal :

p = 20

l = 14

t = 10

Jadi L. Permukaan Balok =2(p+pt+lt)

= 2 x (20×14) + (20×10) + (14 x 10)

= 2 x (280 + 200 + 140)

= 2x620

= 1240 cm²

Jadi, luas permukaan balok tersebut adalah 1240 cm².

Contoh Rumus dan Soal Menghitung Volume Balok

Volume balok adalah ukuran ruang yang dibatasi oleh sisi-sisi balok. Untuk menghitung volume balok (V), perlu diketahui panjang, tinggi, dan lebar balok. Rumus volume balok adalah V = p × l × t. Satuan volume balok ditulis dengan kubus, misalnya sentimeter kubik (cm3) dan meter kubik (m3).

Contoh Soal Volume Balok

Sebuah balok berukuran panjang 7 cm, lebar 4 cm, dan tinggi 3 cm. Maka volume balok tersebut adalah?

Dikenal:

p = 7 cm; l = 4 cm; t = 3 cm

V = p × w × t

V = 7 × 4 × 3

V = 84 cm³.

Jadi, volume balok tersebut adalah 84 cm³ .

Video Trump Sebut Mahasiswa Tak Bisa Hitung 2+2 tapi Malah ke Harvard

Video Trump Sebut Mahasiswa Tak Bisa Hitung 2+2 tapi Malah ke Harvard