Belajar matematika jangan hanya dibaca tapi latihan mengerjakan contoh soal. Siswa kelas 8 mari mengerjalan contoh soal PAS matematika.
Contoh soal memuat berbagai materi yang telah dijelaskan di kelas. Namun kembali diulas beserta jawaban dan pembahasannya.
Melansir dari Buku Guru Matematika Kelas VIII Kurikulum 2013, setidaknya semester satu mempelajari lima bab yaitu:
SCROLL TO CONTINUE WITH CONTENT
Bab 1 Pola Bilangan
Bab 2 Himpunan
Bab 3 Bentuk Aljabar
Bab 4 Persamaan dan Pertidaksamaan Linear Satu Variabel
Bab 5 Perbandingan
Untuk itu, mari mulai membahas contoh soal PAS Matematika kelas 8 Kurikulum 2013.
1. Perhatikan pola bilangan berikut.
(3, 6), (6, 15), (8, 21)
Pernyataan yang tepat untuk mendapatkan bilangan kedua dari
pasangan bilangan pertama pada pola tersebut adalah ....
A. Ditambah 3
B. Dikalikan 2
C. Dikalikan 2 kemudian ditambah 3
D. Dikalikan 3 kemudian dikurangi 3
Jawaban: D. Dikalikan 3 kemudian dikurangi 3
Pembahasan:
Bilangan ke 1 (3, 6)
Bilangan ke 2 (6, 15)
Angka 6 bisa diperoleh dari (3x3)-3 = 6
Sedangkan angka 15 bisa diperoleh dari (6x3)-3 = 15
Begitupula selanjutnya
2. 10, 30, 50, 70, ..., ..., ...
A. 80, 90, 100
B. 90, 110, 130
C. 100, 200, 400
D. 110, 130, 150
Jawaban: B. 90, 110, 130
Pembahasan:
Pola bilangan yang terbentuk adalah (+20). Sehingga tiga angka berikutnya adalah 70 + 20 = 90
90 + 20 = 110
110 + 20 = 130
3. 2, 3, 8, 11, 16, ..., ..., ...
A. 19, 24, 27
B. 18, 23, 26
C. 20, 25, 28
D. 19, 25, 28
Jawaban: A. 19, 24, 27
Pembahasan:
2, 3, 8, 11, 16
__+1__+5__+3__+5
Suku barisan berikutnya ditambah beda dengan pola yang ter urut +5 +3 +5 sehingga :
2, 3, 8, 11, 16, 19 24 27
__+1__+5__+3__+5__+3__+5__+3
4. Diketahui titik A(3,1), B(3, 5), C(-2, 5). Jika ketiga titik tersebut
dihubungkan akan membentuk
A. Segitiga sama sisi
B. Segitiga sama kaki
C. Segitiga siku-siku
D. Segitiga sembarang
Jawaban: C. Segitiga siku-siku
Untuk pertanyaan nomor 5 - 6 perhatikan koordinat kartesius berikut ini:
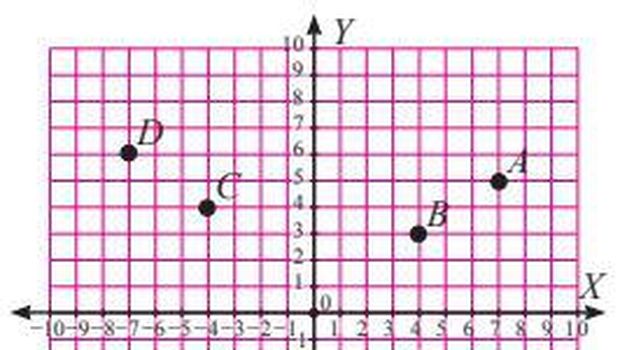 Dok. Buku Kemendikbud Foto: Dok. Buku Kemendikbud Dok. Buku Kemendikbud Foto: Dok. Buku Kemendikbud |
5. Koordinat titik F adalah ....
A. (8, 6)
B. (8, -6)
C. (6, -8)
D. (-8, -6)
Jawaban: D. (-8, -6)
6. Koordinat titik H adalah ....
A. (6, 5)
B. (-6, 5)
C. (6, -5)
D. (-6, -5)
Jawaban: C. (6, -5)
7. Diketahui himpunan P = {1, 2, 3, 5} dan Q = {2, 3, 4, 6, 8, 10}. Jika ditentukan himpunan pasangan berurutan {(1, 2), (2, 4), (3, 6), (5, 10)}, maka relasi dari himpunan P ke himpunan Q adalah ....
A. Kurang dari
B. Setengah dari
C. Dua kali dari
D. Kuadrat dari
Jawaban: B. Setengah dari
Pembahasan bila dilihat himpunan pasangan berurtan:
(1, 2) = 1 adalah setengah dari 2
(2, 4) = 2 adalah setengah dari 4
(3, 6) = 3 adalah setengah dari 6
(5, 10) = 5 adalah setengah dari 10
8. Fungsi f ditentukan oleh f(x) = ax + b. Jika pasangan-pasangan berurutan (p, −3), (−3, q), (r, 2), (2, −2), dan (−2, 6) adalah anggota dari fungsi itu, nilai p, q, dan r adalah ....
A. p = 5, q = 6, dan r = 2
B. p = 3/2, q = 8, dan r = 2
C. p = 5/2, q = 8, dan r = 0
D. p = 3, q = 6, dan r = 3
Jawaban: C. p = 5/2, q = 8, dan r = 0
Pembahasan:
Langkah pertama temukan persamaan fungsi dari dua himpunan pasangan berurutan (2, -2); dan (-2, 6) nelalui bentuk umum dari f(x) = ax + b
Langkah kedua nilai p, q, dan r berdasarkan persamaan fungsi yang diketahui
Jadi, nilai p = 5/2 , q = 8, dan r = 0
9. Diketahui suatu relasi dari himpunan P ke himpunan Q yang dinyatakan dengan himpunan pasangan berurutan {(-1, 2), (1, 4), (3, 6), (5, 8), (7, 10)}. Makan anggota himpunan P adalah ....
A. Himpunan P adalah {-1, 1, 3, 5, 7}
B. Himpunan P adalah {-1, 1, 4, 5, 8}
C. Himpunan P adalah {1, 1, 3, 5, 10}
D. Himpunan P adalah {2, 1, 6, 8, 7}
Jawaban: A. Himpunan P adalah {-1, 1, 3, 5, 7}
Pembahasan:
Karena ditulis himpunan pasangan. Maka anggota himpunan P adalah angka pertama terlebih dahulu sehingga {-1, 1, 3, 5, 7}
10. Gradien garis yang memiliki persamaan y = 2x + 3 adalah ....
A. −3
B. −2
C. 2
D. 3
Jawaban: C. 2
Pembahasan:
Persamaan Garis yang melalui titik (9,-7) dan (3,8) adalah :
y = mx + c
y = 2x +c
m = 2
11. Titik yang terletak pada persamaan 4x − 2y −2 = 0 adalah ....
A. (−2, −3)
B. (−2, 3)
C. (2, −3)
D. (2, 3)
Jawaban: D. (2, 3)
Pembahasan:
4x - 2y - 2 = 0
misal, x = 2
4 . 2 - 2y - 2 = 0
8 - 2y - 2 = 0
6 - 2y = 0
-2y = -6
y = 3
Jadi, (2,3)
12. Persamaan garis yang melalui titik (−3, 6) dan sejajar dengan garis
4y − 3x = 5 adalah ....
A. 4y = 3x + 33
B. 4y = 3x - 33
C. 4y = −3x - 33
D. 4y = 3x + 33
Jawaban: D. 4y = 3x + 33
Pembahasan:
Menentukan gradien (m)
Kita akan menentukan gradien dengan mengubah bentuk persamaan garis menjadi y = mx + c.
4y - 3x = 5
4y = 3x + 5 (bagi kedua ruas dengan 4)
y = 3/4 x + 5/4
Jadi, m = 3/4
Substitusikan titik (-3, 6) dan m
Karena garis saling sejajar, maka m₁ = m₂ = ¾. Substitusikan ke rumus dimana (-3, 6) → (x₁, y₁).
y - y1 = m2(x-x1)
y - 6 = 3/4(x-(-3)
y - 6 = 3/4(x+3) .... (kalikan kedua ruas dengan 4)
4 x (y - 6) = 4 x 3/4(x + 3)
4(y - 6) = 3(x + 3)
4y - 24 = 3x + 9
4y = 3x + 9 + 24
4y = 3x + 33
Kesimpulan: Jadi, persamaan garis yang melalui titik (-3, 6) dan sejajar dengan garis 4y - 3x = 5 adalah 4y = 3x + 33.
13. Harga 3 celana dan 2 baju adalah Rp 280.000. Sedangkan harga 1 celana dan 3 baju di tempat dan model yang sama adalah Rp 210.000. Harga sebuah celana adalah ....
A. Rp65.000,00
B. Rp60.000,00
C. Rp50.000,00
D. Rp45.000,00
Jawaban: B. Rp60.000,00
Pembahasan:
harga celana = x
harga baju = y
3x+2y = 280.000 (×1)
x+3y = 210.000 (×3)
3x+2y = 280.000
3x+9y = 630.000
_______________-
-7y = -350.000
y = -350.000/-7 = 50.000
x+3y = 210.000
x+3(50.000) = 210.000
x+150.000 = 210.000
x = 60.000
Jadi, harga satu celana adalah Rp 60.000,00
14. Selisih umur seorang ayah dengan anaknya 40 tahun. Jika umur ayah tiga kali lipat dari umur anaknya, maka umur anak tersebut adalah ....
A. 10 tahun
B. 15 tahun
C. 20 tahun
D. 25 tahun
Jawaban: C. 20 tahun
Pembahasan:
Misal : x = umur ayah
y = umur anak
Membuat persamaan
Selisih umur ayah dan anak = 40 tahun
x - y = 40 ... pers I
umur ayah = 3 kali umur anak
x = 3y .... pers II
Menentukan umur anak dan ayah
Subtitusi x = 3y ke dalam pers I
x - y = 40
3y - y = 40
2y = 40
y = 40/2
y = 20
Subtitusi y = 20 ke dalam pers I
x - y = 40
x - 20 = 40
x = 40 + 20
x = 60
Jadi umur anak tersebut adalah 20 tahun
15. Jumlah dua buah bilangan cacah adalah 65 dan selisihnya adalah 15. Bilangan terkecil dari dua bilangan tersebut adalah ....
A. 25
B. 30
C. 35
D. 40
Jawaban: A. 25
Pembahasan:
Misal A bilangan 1 dan B bilangan 2
Persamaan:
(I) ..... A + B = 65
(II) .... A - B = 15 +
-----------------------
2A = 80
A = 80/2
A = 40
Bila sudah dapat nilai A = 40, langkah selanjutnya adalah subtitusikan ke dalam persmaan (I) atau persamaan (II).
A + B = 65
40 + B = 65
B = 65 - 40
B = 25
Maka, bilangan terkecil dari kedua bilangan pada soal adalah 25.
Nah, itulah contoh soal PAS Matematika kelas 8 Kurikulum 2013. Selamat belajar detikers!


























































