.webp)
Konsep peluang dalam materi matematika memperkenalkan kita pada istilah kombinasi dan permutasi. Kombinasi adalah cara penyusunan objek tanpa memperhatikan urutan, beda dengan permutasi yang penyusunannya harus berdasarkan urutan.
Susunan {A,B} dan {B,A} dalam kombinasi disebut sama karena tidak mementingkan urutan. Namun dalam permutasi, urutan merupakan hal yang penting sehingga susunan {A,B} dan {B,A} disebut berbeda. Itulah yang membedakan kedua konsep peluang ini.
Pengertian Kombinasi
Dikutip dari Cue Math, kombinasi adalah pilihan yang dibuat dengan mengambil sebagian atau seluruh objek terlepas dari aturannya. Cara pemilihan objek dalam koleksi tersebut tidak mempermasalahkan urutannya.
SCROLL TO CONTINUE WITH CONTENT
Contoh dari kombinasi misal dari 4 bersaudara yaitu Amar (A), Budi (B), Caca (C) dan Dodi (Dodi), diundang 2 perwakilan untuk menghadiri rapat keluarga. Maka, ada berapa pilihan perwakilan yang bisa memenuhi undangan tersebut? Lalu, bagaimana jika yang diundang 3 orang dari 4 bersaudara?
Dapat dikatakan, objek eksperimen dari kasus di atas yaitu = {A,B,C,D} yang diundang perwakilan 2 orang. Dalam kombinasi, jika {A,B} dan {B,A} muncul maka artinya sama saja {A,B} = {B,A}.
Jadi, jika Amir dan Budi terpilih hadir, tentu sama saja artinya jika Budi dan Amir terpilih karena urutan bukan masalah. Hal yang sama berlaku jika yang diundang 3 orang. Jika kombinasi yang muncul {C,A,D} dan {A,C,D}, maka keduanya sama.
Penerapan kombinasi dalam soal peluang biasanya untuk menentukan pemilihan tim atau kelompok, baju, mata pelajaran, makanan. Sedangkan permutasi biasanya pada soal untuk menyusun orang, nomor telepon, nomor rumah, angka, dan warna.
Dalam sebuah lomba, kombinasi digunakan untuk mengambil 3 pemenang secara acak. Sementara itu, permutasi menentukan pemenang dengan urutan juara 1,2, dan 3.
Rumus Kombinasi
Lambang notasi kombinasi adalah C. Jumlah anggota himpunan disebut dengan (n) dan jumlah objek yang harus dipilih disebut (r). Dengan begitu, rumus kombinasi adalah
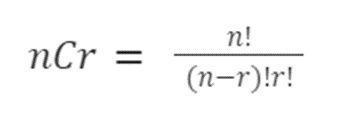 Rumus kombinasi matematika. Foto: Cue Math |
Contoh Soal Kombinasi
Contoh Soal 1
Terdapat himpunan huruf A,B,C,D. Akan dihitung susunan dengan dua huruf tanpa berurutan. Ada berapa banyak susunan dua huruf tersebut?
Dari contoh di atas, kamu bisa menggabungkan dengan manual menjadi AB, AC, AD, BC, BD, CD. Namun jika menggunakan rumus, artinya dengan n = 4 dan r=2 maka
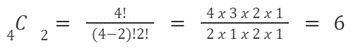 Penyelesaian contoh soal kombinasi 1. Foto: Cue Math |
Contoh Soal 2
Di suatu ujian, setiap siswa harus menjawab 4 dari 7 soal yang ada. Jika seorang siswa secara acak memilih soal untuk dikerjakan, berapa banyak cara atau pilihan soal yang bisa dikerjakan siswa itu?
Dengan n = 7 dan r = 4 maka,
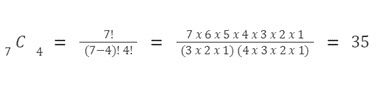 Penyelesaian contoh soal kombinasi 2. Foto: Cue Math |
Demikian pembahasan terkait pengertian kombinasi, perbedaan kombinasi dan permutasi, hingga contoh soal dengan rumus kombinasi. Mudah kan, detikers?
(twu/twu)
