.webp)
Determinan matriks merupakan selisih antara perkalian elemen-elemen pada diagonal utama dengan perkalian elemen-elemen pada diagonal sekunder. Determinan matriks hanya dapat dicari dengan matriks persegi. Determinan dari matriks A dapat ditulis det(A) atau |A|.
Determinan matriks dapat ditemukan dalam matriks persegi ordo 2x2 dan 3x3. Berikut penjelasannya dikutip dari emodul matematika kemdikbud kelas XI:
Jenis determinan matriks dan contoh soal
SCROLL TO CONTINUE WITH CONTENT
1. Determinan Matriks Persegi Berordo 2x2
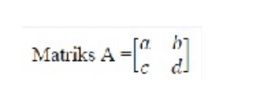 Determinan matriks. Foto: emodul matematika kelas xi |
Hasil kali elemen-elemen diagonal utama dikurangi hasil kali elemen-elemen diagonal samping disebut determinan matriks A. Atau dapat dituliskan degan det A = ad - bc
Contoh soal determinan matriks dengan ordo 2x2 adalah sebagai berikut
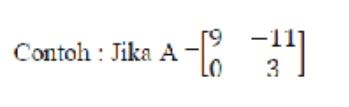 Determinan matriks. Foto: emodul matematika kelas xi |
Notasi determinan matriks A adalah atau det A = ad - bc maka det A =(9.3)-((-11).0) = 27
2. Determinan Matriks Persegi Berordo 3x3
Sama dengan determinan matriks ordo 2x2, dalam mencari determinan matriks A digunakan cara diagonal utama dikurangi hasil kali elemen-elemen diagonal samping. Namun, pada matriks persegi berordo 3x3 memiliki cara yang berbeda. Berikut penjabarannya
 Determinan matriks. Foto: emodul matematika kelas xi |
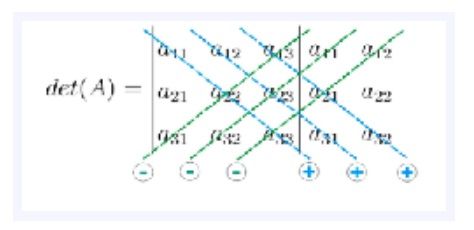
Dalam matriks persegi ordo 3x3, cara menghitung determinan ialah
Determinan A
|A|=(a11.a22.a33)+(a12.a23.a31)+(a13.a21.a32)-(a13.a22.a31)-(a11.a23.a32 )-(a12.a21.a33)
Contoh soal mencari determinan matriks persegi dengan ordo 3x3 adalah sebagai berikut
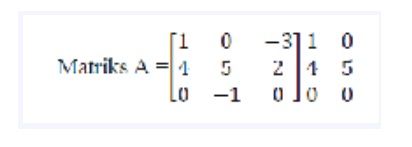 Determinan matriks. Foto: emodul matematika kelas xi |
Cara menentukan det A dari matriks ordo 3x3 adalah sebagai berikut
Determinan A = (1.5.0)+(0.2.0)+((-3).4.0)-((-3).5.0)-(1.2.(-1))- (0.4.0)
=0 + 0 + 0 - 0 -(-2)-0
= 2
Itulah rumus determinan matriks dan contoh soalnya. Mudah bukan?
(row/row)
