Menghitung Luas Trapesium dengan Rumus serta Contoh Soal

Anak dan soal-soal matematika — Bagaimana cara menghitung luas trapesium? Artikel ini akan menjawabnya (Foto ilustrasi: Thikstock)

Jakarta -

Trapesium adalah salah satu bangun datar berbentuk segi empat, yang mempunyai sepasang sisi sejajar, tapi tak sama panjang. Trapesium disebut juga trapezoid. Trapesium mempunyai sua sisi yang sejajar, maka trapesium termasuk bangun ruang dua dimensi.

Sebuah trapesium pasti mempunyai paling tidak, sepasang sisi sejajar yang tidak harus horisontal. Pasangan sudut yang menggunakan satu sisi sejajar sebagai kaki sudut bersama, disebut dengan pasangan sudut alas.

Seperti bangun segi empat lainnya, trapesium juga memiliki empat sudut. Uniknya dibanding yang lain, dalam sebuah trapesium bisa terdapat dua hingga tiga macam sudut sekaligus.

Bisa terdapat sudut lancip (sudut kurang dari 90°), sudut siku-siku (sudut 90°), dan sudut tumpul (sudut lebih dari 90°). Jumlah sudut itu tergantung dengan jenis trapesiumnya.

SCROLL TO CONTINUE WITH CONTENT

Trapesium dibedakan menjadi 3 macam, yaitu trapesium sembarang, trapesium sama kaki, dan trapesium siku-siku.

Dikutip dari modul Matematika Geometri Datar dan Ruang karya Agus Suharja, dkk. berikut adalah jenis-jenis, beserta sifat trapesium.

1. Trapesium Sembarang

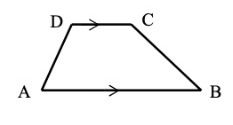Trapesium sembarang Foto: dok. modul Matematika karya Agus Suharja, dkk.

Trapesium sembarang adalah trapesium yang sisi-sisinya memiliki panjang yang berbeda.

AB sejajar dengan DC
AD dan BC disebut kaki trapesium
AB merupakan sisi terpanjang, disebut dengan alas trapesium

2. Trapesium Sama Kaki

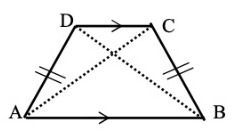Trapesium sama kaki Foto: dok. modul Matematika karya Agus Suharja, dkk.

Trapesium sama kaki adalah trapesium yang kaki-kakinya sejajar, atau sisi tegaknya sama panjang. Sudutnya tidak ada yang berbentuk siku-siku.

AB sejajar dengan DC,
AB sama dengan BC
DAC sama dengan CBA
AC sama dengan BD

3. Trapesium Siku-siku

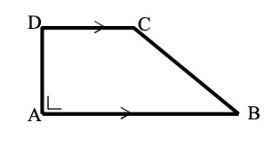Trapesium siku-siku Foto: dok. modul Matematika karya Agus Suharja, dkk.

Trapesium siku-siku adalah trapesium yang salah satu sudutnya membentuk sudut siku-siku 90°.

DC sejajar dengan AB
DAB merupakan bentuk sudut siku-siku.

Sifat-sifat Trapesium

Sebelum membahas luas trapesium, kita perlu mengingat kembali sifat-sifat trapesium:

Masing-masing pasangan sudut saling berdekatan, di antara dua sisi sejajar suatu trapesium saling berpelurus.
Pasangan sudut alas trapesium sama kaki, dan sama besar.
Diagonal trapesium sama kaki, dan sama panjang.

Rumus Trapesium

Gabungan dua trapesium, akan membentuk suatu bangun jajar genjang. Jika kita mengingat luas jajar genjang, maka diperoleh, luas trapesium = ½ x luas jajar genjang

Rumus luas trapesium = ½ (a + b) t

Keterangan:
a = panjang sisi sejajar yang pendek
b = panjang sisi sejajar yang panjang
t = tinggi

Sedangkan, untuk menghitung keliling trapesium, kita hanya perlu menambahkan semua sisi-sisinya saja.

Rumus keliling trapesium = a + b + c + d

Contoh 1
Diketahui sebuah trapesium memiliki a =8 , b = 6 , dan t= 3 , Berapakah luas trapesium tersebut?
Penyelesaian:
L = ½ (a + b) t
L = ½ (8+6) 3
L = 21 cm²

Contoh 2
Masing-masing sisi sejajar trapesium adalah 30 cm , dan 14 cm, dengan tinggi 8 cm. Hitunglah luas trapesium tersebut!
L = ½ x jumlah panjang sisi sejajar x tinggi
L= ½ x (30+14) x 8
L = ½ x 44 x 8
L = 176 cm²

Itu tadi penjelasan mengenai trapesium dan cara menghitung luasnya. Ternyata mudah bukan detikers? Selamat belajar!