.webp)
Integral merupakan operasi kebalikan dari diferensial atau biasa disebut juga dengan antidiferensial. Salah satu bentuk integral yakni integral tak tentu. Seperti apa contoh soalnya?
Integral tak tentu bisa dikatakan sebuah fungsi baru yang memiliki turunan dari fungsi asli. Adapun cara menghitung soal integral tak tentu adalah dengan rumus berikut ini.
Rumus Integral Tak Tentu
SCROLL TO CONTINUE WITH CONTENT
Untuk mengerjakan soal integral tak tentu, perlu diketahui rumusnya terlebih dahulu.
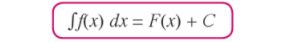 Foto: Repro buku kumpulan soal Think Smart Matematika |
Keterangan:
Κ = operasi antiturunan atau lambang integral
C = suatu konstanta real
f(x) = turunan (diferensial) dari f(x) + C
Sifat-Sifat Integral Tak Tentu
Adapun untuk mengenali contoh soal integral tak tentu, wajib memahami sifat-sifat integral tak tentu. Di antaranya:
 Sifat Integral Tak Tentu Foto: Repro buku kumpulan soal Think Smart Matematika |
Contoh Soal Integral Tak Tentu
Berikut ini contoh soal integral tak tentu, dikutip dari buku kumpulan soal "Think Smart Matematika" oleh Gina Indriani.
1) Perhatikan contoh soal integral berikut ini.
Tentukan:
a. Hitunglah Κ 2 dx
b. Tentukan nilai dari Κ x dx
jawaban:
a. Turunan dari 2x + C adalah 2.
Jadi, Κ 2 dx = 2x + C.
b. Turunan dari 1/2 x2 + C adalah x.
Jadi, Κ x dx = 1/2 x2 + C.
2) Tentukan nilai integral berikut ini!
a. Κ 4 dx
b. Κ x2 dx
c. Κ 6x2 dx
d. Κ (x + 2)2 dx
e. Κ (4x2+ 2x - 1) dx
Jawaban:
a. Κ 4 dx = 4x + C
b. Κ x2 dx = ...
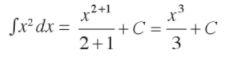 jawaban contoh soal integral tak tentu 2b Foto: Repro buku kumpulan soal Think Smart Matematika |
c. Κ 6x2 dx =
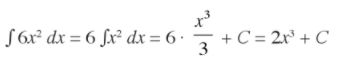 jawaban contoh soal integral tak tentu 2c Foto: Repro buku kumpulan soal Think Smart Matematika |
d. Κ (x + 2)2 dx = Κ (x2 + 4x + 4) dx
= Κ x2 dx + Κ 4x dx + Κ4 dx
= 1/3 x3 + 2x2 + 4x + C.
e. Κ (4x2+ 2x - 1) dx = Κ 4x2 dx + Κ 2x dx - Κ 1 dx
= 4/3 x3 + x2 - x + C.
Itulah contoh soal integral tak tentu beserta pembahasannya. Selamat belajar detikers!
(erd/erd)
