.webp)
Akar kuadrat sering muncul dan dipelajari oleh siswa/siswi sekolah sebagai pelajaran dasar matematika. Akar kuadrat atau akar pangkat dua berfungsi sebagai penyelesaian masalah faktorisasi sebuah persamaan.
Lalu, bagaimana cara menghitung akar kuadrat dan juga penjelasan contoh soalnya? Kenali metodenya di bawah ini.
Apa itu Akar Kuadrat?
Dikutip dari buku yang berjudul Magic Math - Kuadrat, Akar Kuadrat, dan Akar Pangkat Tiga (2013) oleh Tim Magic Math100, akar kuadrat adalah kebalikan dari kuadrat. Jika kuadrat dilambangkan dengan angka 2 dengan posisi agak ke atas, maka akar kuadrat dilambangkan dengan lambang √.
SCROLL TO CONTINUE WITH CONTENT
Cara Mencari Akar Kuadrat
Dilansir dari e-paper yang berjudul Metode untuk Menentukan Akar-akar Persamaan Kuadrat oleh Nabilla Shafira, berikut adalah cara alternatif menentukan akar-akar persamaan kuadrat.
1. Memfaktorkan
Untuk menyelesaikan persamaan kuadrat dengan cara memfaktorkan, perlu diperhatikan hal-hal berikut:
Persamaan dinyatakan dalam bentuk baku sehingga salah satu ruasnya adalah nol. Yaitu: ax² + bx + c = 0 atau 0 = ax² + bx + c
Kemudian bentuk ax² + bx + c difaktorkan, dengan menggunakan sifat; jika pq = 0, maka p = 0, dan q = 0, sehingga langkah penyelesaiannya seperti berikut:
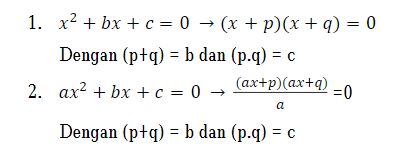 Foto: Nabilla Shafira/via researchgate.net |
2. Melengkapkan Kuadrat Sempurna
Untuk menyelesaikan persamaan kuadrat ax² + bx + c = 0 dengan melengkapi kuadrat sempurna, ditempuh langkah-langkah berikut ini:
- Koefisien x² yaitu a adalah 1 atau dibuat menjadi 1
- Persamaan dinyatakan dalam bentuk x² + mx = n
- Kedua ruas persamaan ditambah dengan (1/2 koefisien x²)
- Persamaan dinyatakan dalam bentuk (x + p)² = q
- (x + p)² = q ↔ x + p = ± √q
3. Rumus ABC
Untuk menyelesaikan persamaan kuadrat dengan rumus, perlu diperhatikan hal-hal berikut:
- Persamaan harus dinyatakan dalam bentuk baku persamaan kuadrat, yaitu ax² + bx + c = 0.
- Tentukan nilai a, b, dan c
Gunakan rumus penyelesaian persamaan kuadrat berikut ini:
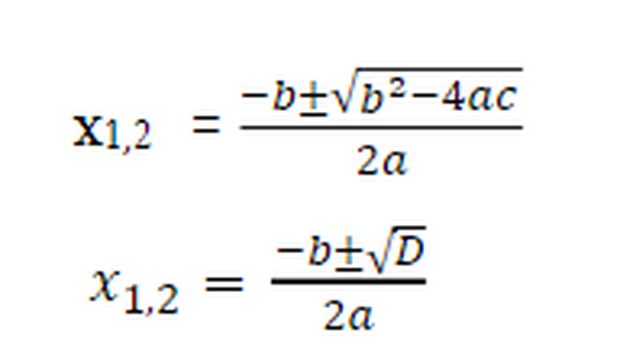 Rumus ABC untuk menghitung persamaan kuadrat. Foto: Nabilla Shafira/via researchgate.net |
Dari rumus di atas tampak bahwa penyelesaian atau akar-akar suatu persamaan kuadrat sangat ditentukan oleh nilai b² - 4ac. Bentuk b² - 4ac disebut diskriminan dari persamaan kuadrat ax² + bx + c = 0 dn dilambangkan dengan huruf D, sehingga D = b² - 4ac.
Pemberian nama diskriminan D = b² - 4ac masuk akal, sebab nilai D = b² - 4ac inilah yang membedakan (mendiskriminasikan) jenis akar-akar suatu persamaan kuadrat.
Dari rumus ABC diatas, diperoleh hubungan:
 Hasil hubungan persamaan kuadrat. Foto: Nabilla Shafira/via researchgate.net |
Jenis akar-akar persamaan kuadrat:
- D ≥ → akar-akarnya real/nyata
- D > 0 → akar-akarnya real dan berlainan
- D = 0 → akar-akarnya real dan kembar
- D < 0 → akar-akarnya imajiner/tidak real/khayal
4. Alternatif Lain
Terlebih dahulu menentukan tanda dari akar-akar persamaan kuadrat sebelum menentukan akar-akar persamaan kuadrat. Aturan tanda dari akar-akar persamaan kuadrat adalah sebagai berikut:
Pada persamaan ax² + bx + c = 0, jika a dan c memiliki tanda yang berlawanan maka kedua akar memiliki tanda yang berlawanan.
Pada persamaan ax² + bx + c = 0, jika a dan c memiliki tanda yang sama, maka:
a. Jika a dan b memiliki tanda yang sama maka akar-akar persamaan kuadrat merupakan akar-akar yang negatif.
b. Jika a dan b memiliki tanda yang berlawanan, maka akar-akar persamaan kuadrat merupakan akar-akar yang positif.
Setelah menentukan aturan tanda, maka persamaan kuadrat dapat diselesaikan.
Contoh Soal Akar Kuadrat dan Penjelasannya
Berikut adalah contoh soal yang dikutip dari buku berjudul Rumus Lengkap Matematika SD oleh Drs. Faturochman:
Contoh Soal Akar Kuadrat 1
 Contoh soal akar kuadrat. Foto: Drs. Faturochman/ dok. e-book Rumus Lengkap Matematika SD |
Contoh Soal Akar Kuadrat 2
 Contoh soal kuadrat. Foto: Drs. Faturochman/dok. e-book Rumus Lengkap Matematika SD |
Demikian pembahasan mengenai akar kuadrat lengkap dengan soal dan cara menghitungnya. Semoga bermanfaat.
(khq/khq)
