Rumus Limit Fungsi Trigonometri: Contoh Soal dan Cara Mengerjakannya

Detikers pernah mendengar rumus limit fungsi trigonometri? Nampaknya kalau bicara soal matematika itu rumit ya?

Namun kenyataannya materi dalam pelajaran matematika ini bisa dipelajari, kok! Pertama-tama, kita bahas terlebih dahulu pengertian dari limit fungsi trigonometri.

Pengertian Limit Fungsi Trigonometri

Limit fungsi trigonometri adalah nilai yang dicapai oleh suatu fungsi trigonometri ketika variabelnya mendekati suatu nilai tertentu.

Limit ini dapat didefinisikan dengan menggunakan rumus limit matematika.

Pada modul Matematika Peminatan Kementerian Pendidikan dan Kebudayaan (Kemdikbud) dijelaskan bahwa limit trigonometri adalah nilai terdekat suatu sudut pada fungsi trigonometri.

Penghitungannya bisa langsung disubstitusi seperti limit fungsi aljabar, tetapi ada fungsi trigonometri yang harus diubah terlebih dahulu ke identitas trigonometri untuk limit tak tentu.

Trigonometri yang biasa kita gunakan ialah:

• Sinus (sin)
• Tangen (tan)
• Cosinus (cos)
• Cotongen (cot)
• Secan (sec)
• Cosecan (csc)

Contoh:

1. Limit sin x ketika x mendekati 0 adalah 0, yang dapat dituliskan sebagai:
   lim sin x = 0, x -> 0
2. Limit cos x ketika x mendekati 90 derajat adalah 0, yang dapat dituliskan sebagai:
   lim cos x = 0, x -> 90

Limit fungsi trigonometri sering digunakan dalam menentukan batas-batas integral, menyelesaikan persamaan diferensial, dan memahami sifat-sifat suatu fungsi trigonometri.

Manfaat Limit Trigonometri

Ada beberapa manfaat dari penggunaan limit trigonometri, antara lain:

1. Membantu Menentukan Batas-batas Integral

Limit trigonometri sering digunakan dalam menentukan batas-batas integral suatu fungsi. Dengan menggunakan limit, kita dapat menentukan nilai integral suatu fungsi dengan lebih akurat.

2. Membantu Menyelesaikan Persamaan Diferensial

Limit trigonometri juga dapat digunakan dalam menyelesaikan persamaan diferensial yang merupakan persamaan matematika yang menjelaskan bagaimana suatu fungsi berubah terhadap waktu atau variabel lainnya.

3. Membantu Memahami Sifat-sifat Suatu Fungsi Trigonometri

Dengan menggunakan limit, kita dapat memahami sifat-sifat suatu fungsi trigonometri seperti apakah fungsi tersebut terbatas atau tidak, dan apakah fungsi tersebut mengalami perubahan sifat atau tidak pada nilai tertentu.

4. Membantu dalam Perhitungan yang Lebih Akurat

Penggunaan limit dapat membantu dalam perhitungan yang lebih akurat, terutama pada nilai-nilai yang sangat dekat dengan batas tertentu.

Secara keseluruhan, penggunaan limit trigonometri dapat membantu dalam memahami sifat-sifat suatu fungsi trigonometri, menyelesaikan persamaan diferensial, dan menentukan batas-batas integral.

Rumus Limit Trigonometri

Berikut ini adalah beberapa rumus limit trigonometri yang sering digunakan:

1. Limit sin x ketika x mendekati 0 adalah 0, yang dapat dituliskan sebagai:
   lim sin x = 0, x -> 0
2. Limit cos x ketika x mendekati 90 derajat adalah 0, yang dapat dituliskan sebagai:
   lim cos x = 0, x -> 90
3. Limit tan x ketika x mendekati 90 derajat adalah tak terhingga, yang dapat dituliskan sebagai:
   lim tan x = ∞, x -> 90
4. Limit cot x ketika x mendekati 0 derajat adalah tak terhingga, yang dapat dituliskan sebagai:
   lim cot x = ∞, x -> 0
5. Limit sec x ketika x mendekati 90 derajat adalah tak terhingga, yang dapat dituliskan sebagai:
   lim sec x = ∞, x -> 90
6. Limit csc x ketika x mendekati 0 derajat adalah tak terhingga, yang dapat dituliskan sebagai:
   lim csc x = ∞, x -> 0

Perhatikan bahwa rumus limit trigonometri di atas hanya berlaku untuk nilai-nilai x yang mendekati batas tertentu. Jika nilai x tidak mendekati batas tertentu, maka nilai limit dapat berbeda.

Sebagai contoh, jika x mendekati 180 derajat maka limit sin x = 0, x -> 180.

Gunakan metode substitusi untuk menentukan nilai limit fungsi trigonometri berikut ini:

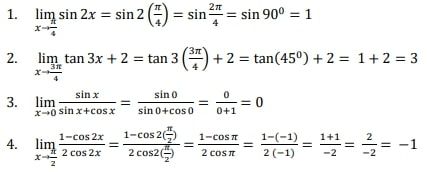Metode Substitusi. Foto: Modul Matematika Peminatan Kemdikbud

Berikut tabel sudut istimewanya:

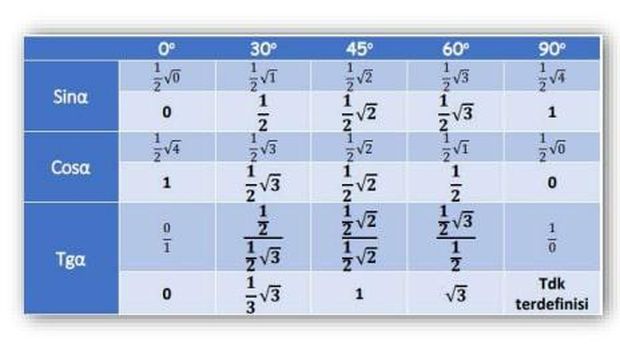Tabel Sudut Istimewa. Foto: Modul Matematika Peminatan Kemdikbud

Setelah diketahui metode substitusi dan sudut istimewanya, gunakan rumus dasar limit fungsi trigonometri sederhana:

Rumus Limit Fungsi Trigonometri. Foto: Modul Matematika Peminatan Kemdikbud

Contoh dan Cara Menghitung Limit Trigonometri

Berikut ini adalah contoh sederhana mengenai cara menghitung limit trigonometri:

Contoh:

Hitunglah limit sin x ketika x mendekati 30 derajat.

Jawaban:

Kita dapat menggunakan rumus sin x = 2 sin (x/2) cos (x/2) untuk menghitung limit sin x.

lim sin x = lim [2 sin (x/2) cos (x/2)]
= 2 lim [sin (x/2)] lim [cos (x/2)]

Kita tahu bahwa limit sin (x/2) ketika x/2 mendekati 0 adalah 0, sehingga limit sin x = 2 * 0 * lim [cos (x/2)]

Sekarang, kita harus menghitung limit cos (x/2) ketika x/2 mendekati 0.

Kita dapat menggunakan rumus cos2 (x/2) + sin2 (x/2) = 1 untuk menghitung limit cos (x/2).

Jika x/2 mendekati 0, maka sin (x/2) juga mendekati 0, sehingga cos2 (x/2) + sin2 (x/2) = cos2 (x/2) + 0 = cos2 (x/2).

Dengan demikian, limit cos (x/2) = √(cos2 (x/2)) = √(1) = 1.

Kemudian, limit sin x = 2 * 0 * 1 = 0.

Jadi, limit sin x ketika x mendekati 30 derajat adalah 0.

Cara menghitung limit trigonometri dapat berbeda tergantung pada fungsi yang akan dihitung dan batas yang akan dicari.

Namun, prinsip yang digunakan umumnya sama yaitu dengan menggunakan rumus-rumus trigonometri dan menentukan limit tiap bagian dari rumus tersebut.

Nah detikers, itulah tadi cara mengerjakan limit fungsi trigonometri. Sekarang kamu sudah paham, kan? Semoga artikel ini bisa membantu, ya!

Pesona Wisata Sumenep: Pantai, Sejarah, dan Tradisi

Pesona Wisata Sumenep: Pantai, Sejarah, dan Tradisi