Cara Menghitung dan Rumus Modus, Data Tunggal, Data Kelompok Beserta Contohnya

Saat di bangku sekolah, kita acap kali diminta menyelesaikan soal seputar modus. Sebetulnya, modus adalah data yang sering atau paling banyak muncul. Berikut ini rumus dan beberapa contoh pengaplikasiannya.

Cara Menghitung Modus

Modus biasa digunakan untuk melihat data yang paling banyak muncul. Modus biasa disingkat dengan (Mo). Berikut cara menghitungnya, dilansir dari Rencana Pelaksanaan Pembelajaran Daring SMPN 2 Arungkeke.

• Contoh soal modus 1

Terdapat delapan sepatu dengan harga berikut untuk koleksi terbaru:

Rp 200.000, Rp 310.000, Rp 1.220.000, Rp 650.000

Sedangkan untuk sepatu koleksi lama:

Rp 480.000, Rp 370.000, Rp 200.000, Rp 450.000

Berapa modus dari delapan sepatu tersebut?

Jawab: Modus (Mo) dari harga sepatu tersebut adalah Rp 200.000 karena harga tersebut muncul dua kali.

• Contoh soal modus 2

Berikut adalah data berat badan (dalam kg) siswa laki-laki kelas VIII.2 SMPN 6 Parepare:

47 57 53 50 45 48 52 49 55 57 46 57

Berapa modus dari berat badan siswa laki-laki?

Jawab: Modus dari berat badan siswa laki-laki adalah 57kg karena muncul 3 kali.

Cara Menghitung Modus Data Tunggal

Modus merupakan suatu skor atau nilai yang mempunyai frekuensi paling banyak, dengan kata lain, skor atau nilai yang mempunyai frekuensi maksimal dalam distribusi data. Mencari modus untuk data tunggal dapat dilakukan dengan mudah dan cepat sekali, yaitu hanya dengan memeriksa atau mencari mana diantara skor yang ada yang memiliki frekuensi yang paling banyak. Contoh soal:

• Contoh soal modus data tunggal 1

Sekumpulan data: 2, 3, 4, 4, 5 maka modusnya adalah 4.

• Contoh soal modus data tunggal 2

Sekumpulan data: 3, 3, 3, 4, 4, 5, 5, 5, 6, 9 maka modusnya adalah 3 dan 5.

• Contoh soal modus data tunggal 3

Sekumpulan data: 3, 4, 5, 6, 7 maka modusnya tidak ada.

Cara Menghitung Modus Data Berkelompok

Untuk menemukan modus data berkelompok maka langkah pertama adalah mencari posisi modus. Digunakan anggapan bahwa modus berada pada kelas dengan frekuensi paling banyak, yaitu contohnya pada kelas ke-4 (kelas pendapatan 33 - 38).

Langkah kedua mencari besarnya modus. Bisa menggunakan rumus:

Cara menghitung dan rumus modus. Foto: Anindyadevi Aurellia/detikcom.

Berikut daftar soal modus data berkelompok:

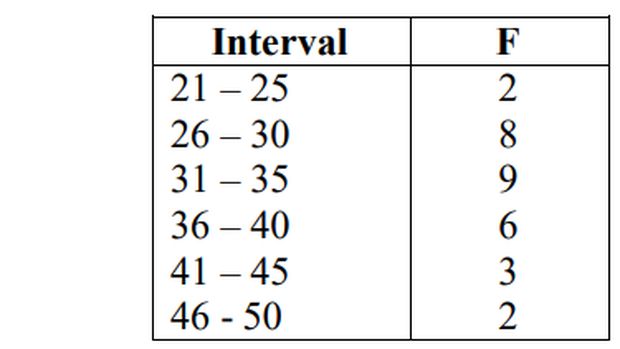
• Contoh soal modus data berkelompok 1

Soal mencari data yang paling banyak atau sering muncul ini dikutip dari Modul Statistika I Wayan Sumandya, M.Pd.

Cara menghitung dan rumus modus. Foto: Anindyadevi Aurellia/detikcom.

Jawab:

Frekuensi paling banyak adalah 9 pada interval 31 - 35.

Jadi kelas modus pada interval 31 - 35.

Tb = 30,5

p = 5

d1 = 9 - 8 = 1

d2 = 9 - 6 = 3

Cara menghitung dan rumus modus. Foto: Anindyadevi Aurellia/detikcom.

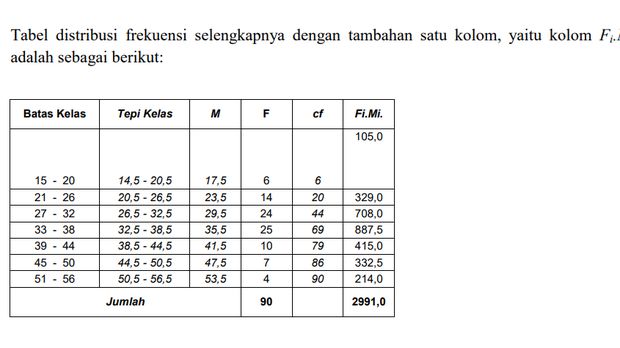
• Contoh soal modus data berkelompok 2

Pertanyaan mencari data modus ini dikutip dari Arif Wibowo dalam bab 3 ringkasan data Pendidikan Statistik UNY

Cara menghitung dan rumus modus. Foto: Anindyadevi Aurellia/detikcom.

Modusnya berapa?

Jawab:

Digunakan anggapan bahwa modus berada pada kelas dengan frekuensi paling banyak, yaitu pada kelas ke-4 (kelas pendapatan 33 - 38). Kemudian cari besarnya modus dengan rumus seperti pada gambar 1.

Dari tabel diketahui:

Tb = 32.5

d1 = 25 - 24 = 1

d2 = 25 - 10 = 15

I = 6,

maka:

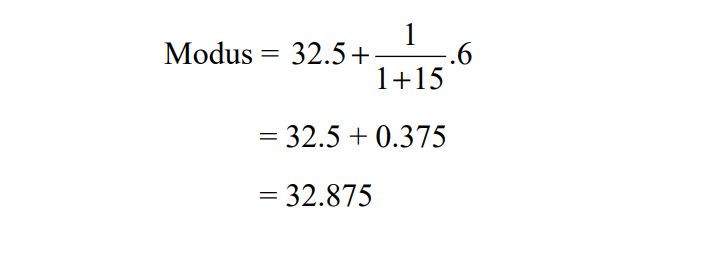Cara menghitung dan rumus modus. Foto: Anindyadevi Aurellia/detikcom.

Pengertian Modus

Tri Hidayati, M.Pd. dkk dalam buku Statistika Dasar menuliskan bahwa Modus memiliki artian sebagai data yang paling sering muncul atau memiliki frekuensi tertinggi dari pengamatan yang diperoleh. Apabila ada satu modus atau satu data yang memiliki frekuensi paling banyak keluar dari data pengamatan, maka disebut sebagai unimodus. Notasi modus adalah Mo.

Manfaat dari Modus

Dilansir dari buku Cerdas Belajar Matematika karya Marthen Kanginan, ada beberapa kelebihan yakni:

• Digunakan untuk data yang diukur dalam skala nominal, ordinal, interval, dan rasio

• Tidak peka terhadap data ekstrim (outliers)

• Cocok untuk data homogen maupun heterogen.

Kekurangan dari Modus

• Kurang dapat menggambarkan mean populasi

• Bisa memiliki dua atau lebih modus.

Contoh Lain Penghitungan Modus

• Cara penghitungan modus 1

Menurut Nata Wirawan dalam buku Cara Mudah Memahami Statistika Ekonomi dan Bisnis, modus bisa diketahui bila datanya telah disusun dalam tabel frekuensi. Tahapannya adalah:

(1) Menentukan letak modus (LMod). Modus terletak pada kelas dengan frekuensi terbesar

(2) Menghitung modus

Modus data berkelompok dapat dihitung dengan rumus:

Cara menghitung dan rumus modus. Foto: Anindyadevi Aurellia/detikcom.

• Cara penghitungan modus 2

Sutartyat Trisnamansyah dalam Statistika Deskriptif menjelaskan ketika terdapat data mean, median, dan modus yang berbeda. Jika distribusi data tidak simetriks, yaitu ketika mean lebih besar dari median dan modus, atau ketika mean lebih kecil dari median, dan modus tidak sama, maka terdapat hubungan empiris antara mean, median dan modus sebagai berikut:

Modus = mean - 3(mean-media)

Bagaimana Cara Mencari Modus Data?

Terdapat empat prinsip menurut Sutartyat, ia menerapkan bahwa apabila ada satu modus atau satu data yang memiliki frekuensi paling banyak keluar dari data pengamatan, maka disebut sebagai unimodus. Jika dua mode data maka disebut bimodus atau bimodal, dan lebih dari itu disebut multimodal. Empat keterangannya yakni:

1. Modus dari suatu kumpulan data adalah nilai yang muncul dengan frekuensi terbesar.

2. Frekuensi terbesar dapat terjadi pada dua atau lebih nilai yang berbeda.

Jika distribusi data tidak simetriks, maka terdapat hubungan empiris antara mean, median dan modus sebagai berikut:

Modus = mean - 3(mean-media)

3. Jika data memiliki tepat dua mode, data tersebut bimodal.

Contoh: 3 4 4 4 6 8 8 8 9 10. Mo = 4 dan 8.

4. Jika data memiliki lebih dari dua mode, data tersebut multimodal.

Nah, itulah tadi penjelasan mengenai Modus, lengkap dengan cara menghitung, rumus, dan contoh soalnya. Mudah bukan? Semoga dengan informasi di atas, sudah cukup jelas untuk membantumu mengerjakan soal.

Video: Pelaku Demo Rusuh di Bandung Dapat Kucuran Dana dari Luar Negeri

Video: Pelaku Demo Rusuh di Bandung Dapat Kucuran Dana dari Luar Negeri